Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 98

Considere uma casa cuja parede sul consiste de uma parede de Trombe de 30 cm de espessura, condutividade térmica k = 0,70 W/m.K e difusividade térmica α = 0,44 x 10 - 6 m 2 / s . As variações da temperatura ambiente T e x t e do fluxo de calor q ˙ s o l a r incidente sobre a superfície sul vertical, ao longo de um dia típico de fevereiro, são dadas na Tab. P5-98, para intervalos de três horas. A parede de Trombe tem vidraça única, com produto de absortividade de transmissividade κ = 0,76 (ou seja, 76% da energia solar incidente é absorvida pela superfície exposta), e o coeficiente médio combinado de transferência de calor para perdas de calor da parede de Trombe para o ambiente é h e x t = 3,4     W / m ² . K . O interior da casa é mantido a T i n t = 20   ° C durante o tempo todo, e o coeficiente médio combinado de transferência de calor para perdas de calor na superfície interna é h i n t = 9,1     W / m ² . K . Além disso, as aberturas da parede de Trombe são mantidas fechadas, assim a transferência de calor entre o ar da casa e as paredes ocorre somente através da superfície interna. Partindo do princípio de que a temperatura da parede varia linearmente entre 20 °C na superfície interna e 0 °C na superfície externa às 7 horas, e utilizando o método explícito das diferenças finitas com espaçamento nodal uniforme de Δx = 5 cm, determine a distribuição ao longo da espessura da parede de trombe após 6, 12, 18, 24, 30, 36, 42 e 48 horas e trace os resultados. Além disso, determine a quantidade líquida de calor transferido para a casa a partir dessa parede de 2,8 m de altura e 7 m de comprimento durante o primeiro dia.

Passo 1

Vamos analisar juntos o enunciado e entender o que esse problema quer de você.

Devemos resolver esse problema transiente pelo método das diferenças finitas e integração temporal utilizando um método explícito.

O enunciado afirma que temos um espaçamento nodal de Δ x   =   5   c m e, partir dessa determinação, devemos estabelecer o número de nós M (e consequentemente, de equações) que utilizaremos para resolver este problema.

O número de nós (M) pode ser estabelecido ao se dividir a espessura da parede ( 30   c m ) pelo espaçamento nodal estabelecido, acrescido de uma unidade:

M = L Δ x + 1 =   30   c m 5   c m   + 1 = 6 + 1 = 7

Pra facilitar nossas futuras análises, fique de olho nesse esquema ilustrativo pra entender o que tá acontecendo:

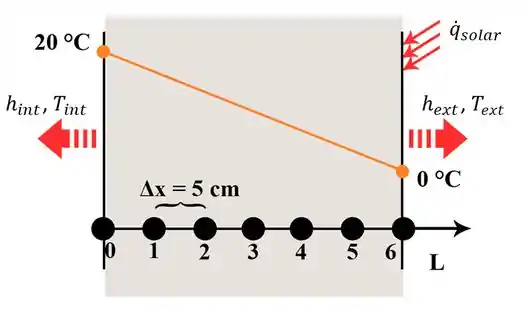
Vamos analisar a figura.

Primeiro, note que as temperaturas iniciais variam linearmente da superfície interna até a externa, indo de 20 ° C a 0 ° C . Elas serão posteriormente calculadas.

Além disso, tanto a temperatura externa quanto a incidência dos raios solares não são constantes, e devemos nos atentar aos tempos que estamos analisando a partir dos critérios estabelecidos pela Tabela P5-98. Por conta disso, as condições de contorno serão constantemente mudadas, o que vai interferir na nossa resposta.

Antes da gente partir para os próximos passos, vou enumerar uma sequência lógica do que a gente vai fazer pra resolver a questão:

  1. Primeiro, vamos explicitar as equações dos nós internos;
  2. Depois, vamos explicitar as equações dos nós mais externos, ou seja, as condições de contorno do problema;
  3. Calcular o passo temporal Δ t de forma a manter o critério de estabilidade da solução;
  4. Calcular as temperaturas ao longo do tempo em cada uma das sete posições estabelecidas;
  5. Calcular a quantidade líquida de calor que atravessa a parede em 24h a partir das temperaturas calculadas.

Para resolver esse problema, recomendo fortemente que você use o Excel pra realizar as contas e traçar o gráfico que a questão pede. Não requer um conhecimento avançado, só mesmo o uso de fórmulas. É a abordagem que vou utilizar aqui e facilita nosso trabalho!

Ok, agora depois de ser bombardeado com tantas informações, vamos organizar direitinho as propriedades fixas que vamos utilizar nesse problema pra gente não se perder:

k   =   0,70   W / m . K   α   =   0,44 x 10 - 6 m 2 / s   κ   =   0,76 T i n t = 20   ° C h i n t = 9,1     W / m ² . K h e x t = 3,4     W / m ² . K .

Passo 2

A partir da discretização do balanço diferencial de calor para uma placa plana transiente sem geração, podemos obter a seguinte equação geral para os nós internos:

T m i + 1 =   τ T m - 1 i + T m + 1 i + ( 1 - 2 τ ) T m i

Sendo m o número do nó e i o índice temporal.

Além disso, τ é o número de Fourier, expresso por:

τ =   α ∆ t ∆ x ²

Que será devidamente calculado quando encontrarmos o passo ∆ t .

Vamos agora organizar nossos cinco nós internos:

Nó 1 (m=1): T 1 i + 1 =   τ T 0 i + T 2 i + ( 1 - 2 τ ) T 1 i

Nó 2 (m=2): T 2 i + 1 =   τ T 1 i + T 3 i + ( 1 - 2 τ ) T 2 i

Nó 3 (m=3): T 3 i + 1 =   τ T 2 i + T 4 i + ( 1 - 2 τ ) T 3 i

Nó 4 (m=4): T 4 i + 1 =   τ T 3 i + T 5 i + ( 1 - 2 τ ) T 4 i

Nó 5 (m=5): T 5 i + 1 =   τ T 5 i + T 6 i + ( 1 - 2 τ ) T 5 i

Passo 3

Como a superfície interna está submetida a uma condição de contorno de convecção, podemos utilizar a seguinte equação explicita para calcular a temperatura no nó 0:

T 0 i + 1 =   1 - 2 τ - 2 τ h i n t ∆ x k T 0 i + 2 τ T 1 i + 2 τ h i n t ∆ x k T i n t

Como h i n t , ∆ x , k   e T i n t são constantes, podemos substituir na equação:

T 0 i + 1 =   1 - 2 τ - 2 τ ( 9,1   W m 2 . K ) ( 0,05   m ) 0,70   W / m . K T 0 i + 2 τ T 1 i + 2 τ ( 9,1   W m 2 . K ) ( 0,05   m ) 0,70   W / m . K T i n t

→ T 0 i + 1 =   1 - 2 τ - 2 τ ( 0,65 ) T 0 i + 2 τ T 1 i + 2 τ ( 0,65 ) ( 20 )

→ T 0 i + 1 =   1 - 2 τ - 1,3 τ T 0 i + 2 τ T 1 i + 26 τ

→ T 0 i + 1 =   1 - 3,3 τ T 0 i + τ ( 2 T 1 i + 26 )

Passo 4

Como a superfície externa está submetida condições de contorno de convecção e ao fluxo de calor incidente, podemos utilizar a seguinte equação explicita para calcular a temperatura no nó 6:

T 6 i + 1 =   1 - 2 τ - 2 τ h e x t ∆ x k T 6 i + 2 τ T 5 i + 2 τ h e x t ∆ x k T e x t i + 2 τ κ q ˙ s o l a r ∆ x k    

Como h e x t , ∆ x , k   e κ são constantes, podemos substituir na equação:

T 6 i + 1 =   1 - 2 τ - 2 τ ( 0,24 ) T 6 i + 2 τ T 5 i + 2 τ ( 0,24 ) T e x t i + 2 τ ( 0,76 ) q ˙ s o l a r ( 0,05 ) 0,7

→ T 6 i + 1 =   1 - 2 τ - 2 τ ( 0,24 ) T 6 i + 2 τ T 5 i + 2 τ 0,24 T e x t i + 2 τ ( 0,054 ) q ˙ s o l a r  

→ T 6 i + 1 =   1 - 2 τ - 0,48 τ T 6 i + 2 τ T 5 i + 0,48 τ T e x t i + 0,108 τ q ˙ s o l a r  

→ T 6 i + 1 =   1 - 2,48 τ T 6 i + τ ( 2 T 5 i + 0,48 T e x t i + 0,108 q ˙ s o l a r )  

Passo 5

Devemos, agora, calcular ∆ t a partir do critério de estabilidade. Isso exige analisar o menor coeficiente primário do sitema. Os nós de contorno são mais restritivos que os internos, e o menor coeficiente entre eles é o que acompanha T 0 i .

Portanto, devemos ter:

1 - 3,3 τ   ≥ 0   →   - 3,3 τ   ≥ - 1   →   τ ≥   1 3,3   → τ ≤   1 3,3

Mas, como τ =   α ∆ t / ∆ x ² , temos:

  α ∆ t ∆ x ² ≤   1 3,3 → ∆ t ≤   ∆ x 2 α 3,3 = ( 0,05   m ) ² ( 0,44 x 10 - 6 m 2 / s ) ( 3,3 )   = 1722   s

Ou seja, qualquer passo de integração menor do que 1722 s pode ser utilizado. Por conveniência, vamos utilizar ∆ t = 900   s , que são 15 m i n . Assim:

τ =   α ∆ t ∆ x ² =   ( 0,44 x 10 - 6 m 2 / s ) ( 900   s ) ( 0,05   m ) ² = 0,158

Passo 6

Agora, vamos deixar claro quais são os valores de q ˙ s o l a r e T e x t i ao longo do tempo. Vamos analisar a Tabela P5-98:

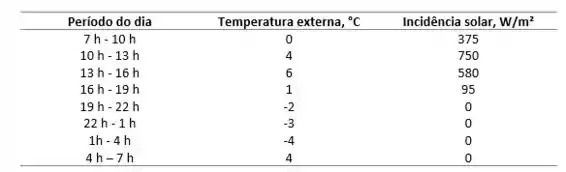
Podemos perceber que a temperatura externa e a incidência solar variam a cada 3 h, ou seja, a cada 12 passos de 15 min (900 s).

Vamos colocar aqui as equações que vamos utilizar na resolução do problema:

T 0 i + 1 =   1 - 3,3 τ T 0 i + τ ( 2 T 1 i + 26 )

T 1 i + 1 =   τ T 0 i + T 2 i + ( 1 - 2 τ ) T 1 i

T 2 i + 1 =   τ T 1 i + T 3 i + ( 1 - 2 τ ) T 2 i

T 3 i + 1 =   τ T 2 i + T 4 i + ( 1 - 2 τ ) T 3 i

T 4 i + 1 =   τ T 3 i + T 5 i + ( 1 - 2 τ ) T 4 i

T 5 i + 1 =   τ T 5 i + T 6 i + ( 1 - 2 τ ) T 5 i

T 6 i + 1 =   1 - 2,48 τ T 6 i + τ ( 2 T 5 i + 0,48 T e x t i + 0,108 q ˙ s o l a r )

Lembrando que τ = 0,158 .

Lembre-se de que as temperaturas iniciais às 7 h variam linearmente com o espaço de 20 a 0 ° C nos nós 0 a 5. A mudança de temperatura entre dois nós vizinhos pode ser calculada como:

∆ T   =   20   ° C - 0   ° C 6 = 3,33   ° C

Ou seja, há uma queda de 3,33 °C em cada nó. Assim, as temperaturas iniciais são:

T 0 0 = 20   ° C

T 1 0 = 16,67   ° C

T 2 0 = 13,34   ° C

T 3 0 = 10,01   ° C

T 4 0 = 6,68   ° C

T 5 0 = 3,35   ° C

T 6 0 = 0   ° C

A partir dessas temperaturas inicias e das equações para os nós, é possível fazer várias iterações e calcular as temperaturas ao longo do tempo. Segundo o enunciado, nossa análise deve ir até 48 h (17800 s).

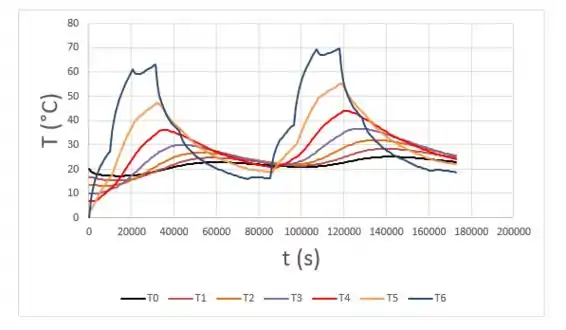
Agora, vamos determinar as temperaturas em 6, 12, 18, 24,30, 36, 42 e 48 h, segundo determina o enunciado:

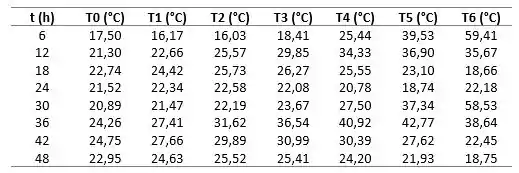
Passo 7

Agora, devemos calcular a quantidade líquida de calor que atravessa a parede durante um dia (24 h).

Primeiro, devemos calcular a quantidade líquida de calor em cada passo de 15 min:

Q I = h i n t A ( T 0 i - T 0 i - 1 ) / 2 - T i n t ∆ t

Sendo A   = 2,8   m   7   m = 19,6   m ²  

Então, para encontrar a quantidade líquida de calor que atravessou a parede durante 24 h, basta somar as taxas até 86400 s.

Logo,

Q = 6068   k J

Resposta

As respostas estão demonstradas nos passos 6 e 7.

Ver Outros Exercícios desse livro