Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 8

Considere a condução de calor permanente unidimensional em uma parede plana com geração de calor variável e condutividade térmica constante. A rede nodal do meio consiste dos nós 0, 1, 2, 3 e 4, com espaçamento nodal uniforme de ∆ x . Usando a forma de diferenças finitas da derivada primeira (e não a abordagem do balanço de energia), obtenha a formulação de diferenças finitas dos nós de contorno para caso de fluxo de calor uniforme q ˙ 0 no contorno da esquerda (nó 0) e de convecção no contorno do lado direito (nó 4) com coeficiente de convecção h e temperatura ambiente de T ∞ .

Passo 1

Se fizermos a representação do exercício em um desenho com os dados que o enunciado nos deu, temos a seguinte representação:

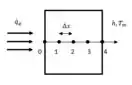
Vamos supor que a parede tenha um comprimento L . Com essa figura conseguimos ver as extremidades da parede e podemos aplicar as condições de contorno, que representarão o que está acontecendo em cada ponto. Cada ponto desse tem uma temperatura T m .

Passo 2

As condições de contorno da parede para o lado esquerdo onde só ocorre condução e lado direito que ocorre convecção, pois está em contato com o ambiente são dadas por essas equações:

L a d o   e s q u e r d o   ( n ó   0 ) →   - k d T 0 d x = q ˙ 0

L a d o   d i r e i t o   ( n ó   4 ) →   - k d T L d x = h [ T L - T ∞ ]

Passo 3

Agora precisamos equacionar as formulações de diferenças finitas das extremidades da parede para podermos aplicar nas condições de contorno:

d T d x m = 0 = T 1 - T 0 ∆ x

d T d x m = 4 = T 4 - T 3 ∆ x

Resposta

Substituindo as formulações de diferenças finitas nas condições de contorno, chegamos na nossa resposta:

L a d o   e s q u e r d o   ( n ó   0 ) →   - k T 1 - T 0 ∆ x = q ˙ 0

L a d o   d i r e i t o   ( n ó   4 ) →   - k T 4 - T 3 ∆ x = h [ T 4 - T ∞ ]

Ver Outros Exercícios desse livro