Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 118
Considere a condução de calor permanente unidimensional em uma parede plana com geração de calor variável e condutividade térmica constante. A rede nodal do meio consiste de nós com espaçamento nodal uniforme de . A temperatura no contorno da esquerda (nó ) é especificada. Usando a abordagem do balanço de energia, obtenha a formulação de diferenças finitas do nó do contorno do lado direito para o caso de convecção e radiação combinadas com emissividade de , coeficiente de convecção , temperatura ambiente de , e temperatura do meio ao redor de . Além disso, obtenha a formulação de diferenças finitas para taxa de transferência de calor no contorno do lado esquerdo.
Passo 1
A questão possui uma figura representativa que se assemelha a seguinte:
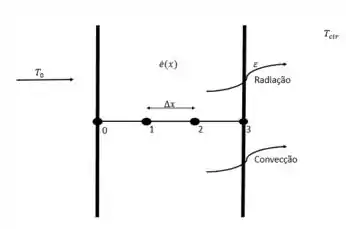
A figura representa a parede plana nas condições descritas no enunciado e devem ser determinadas as formulações de diferenças finitas nos nós e .
Passo 2
Utilizando-se os balanços energéticos, e assumindo a direção de toda forma de transferência de calor ocorrendo em direção aos nós em questão, obtém-se as seguintes formulações de diferenças finitas:
Nó :
Nó :
Resposta
Ei, a resposta está no passo a passo :)