Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 6.Problemas - Ex. 54
Considere o escoamento entre duas grandes placas paralelas isotérmicas separadas por uma distância . A placa superior se desloca a uma velocidade constante e é mantida a uma temperatura enquanto a placa inferior está parada e isolada. As relações para temperatura máxima do fluido, local em que ela ocorre e a equação de fluxo de calor são dadas a seguir:
Que ocorre em
A partir disso, obtenha a relação para taxa volumétrica de geração de calor em W/m3. Expresse o problema de convecção como problema de condução equivalente na camada de óleo. Verifique seu modelo, resolvendo o problema de condução e obtenha a relação para temperatura máxima, que deverá ser idêntica à obtida na análise de convecção.
Passo 1
Em primeiro lugar vamos desenhar nossa situação.
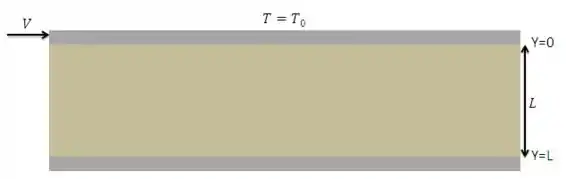
O nosso fluxo é dado por . Como sabemos fluxo representa uma quantidade por tempo que atravessa uma área. Para o nosso caso de transferência de calor energia () por tempo () por área superficial da placa (), considerando sistema internacional.
Como , nossa unidade de fluxo é . Para convertermos fluxo para taxa volumétrica de geração de calor em W/m3 devemos então multiplicar pela área superficial () e dividir pelo volume de fluido ().
Passo 2
Vamos tratar agora o problema como se fosse a condução de calor através do óleo. Como sabemos o fluxo de calor por condução é dado por:
Também sabemos que a temperatura na superfície superior do óleo é e a temperatura na superfície inferior é . Para fazer os deltas vamos considerar que o ponto inicial é em e o final é em . Pelo enunciado sabemos que o fluxo deve ser:
Igualando as duas equações de fluxo:
Integrando de até e de até :
Que é a mesma relação dada pelo enunciado.
Resposta
Ei, a resposta está no passo a passo :)