Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 12.Problemas - Ex. 78
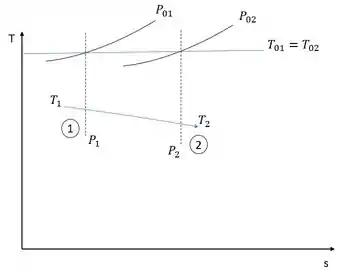
Considere o escoamento permanente e adiabático de ar através de um tubo reto com A = 0,05 m². Na entrada (seção 1), o ar está a 200 kPa (abs), 60°C e 146 . A jusante, na seção 2, o ar está a 95,6 kPa (abs) e 280 . Determine e a variação de entropia para o escoamento. Mostre os pontos de estado estático e de estagnação em um diagrama Ts.
Passo 1
Oi pessoal, tudo bem ?
Vamos às considerações do problema:
Obs: Propriedades do ar (Tabela A.6). ;
Para encontrar o número de Mach:
O c (velocidade do som), é definido como:
Então:
Sabendo do valor de , podemos descobrir a temperatura e pressão de estagnação na seção 1:
Passo 2
Bem, agora usando a primeira lei da termodinâmica, temos:
Assumimos que:
Então:
Mas, sabe-se que , e
Substituindo as considerações na equação da 1ª Lei:
Portanto, para entalpias específicas iguais,
Então:
Passo 3
Bem, agora só resta descobrir o valor de
Por continuidade, temos:
E:
Agora, podemos descobrir a velocidade do som na seção 2, para posterior , e então, a pressão de estagnação na seção 2.
Então:
Agora, substituindo os valores na equação da pressão de estagnação na seção 2:
Passo 4
Para a variação da entropia:
Então:
Resposta
; ; ;
Diagrama Ts:
