Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 100

Considere o escoamento supersônico do ar através de um duto com 6   c m de diâmetro e atrito desprezível. O ar entra no duto a M a 1   =   1,8 , P 01   =   210   k P a e T 01 =   600   K , e é desacelerado pelo aquecimento. Determine a mais alta temperatura com a qual o ar possa ser aquecido pela adição de calor, enquanto a vazão em massa permanece constante.

Passo 1

Vamos começar desenhando um esqueminha do que ta acontecendo!!

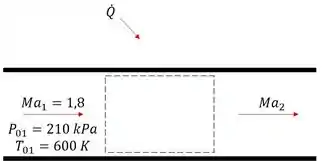
O problema diz que fluido foi desacelerado pelo aquecimento e quer saber a mais alta temperatura T 2 o ar pode ser aquecido, mantendo a vazão constante!

Para isso a gente precisa lembrar que essa temperatura acontece no estado crítico do escoamento, que é quando M a = 1 , logo:

M a 2 = 1

Agora a gente quer encontrar T 2 !!

Passo 2

Aqui a gente tem um escoamento de ar, isso já facilita bastante as coisas, porque para o ar a gente tem uma tabela de funções no final do livro!!

Da tabela A - 15 tiramos:

Para M a 1 = 1,8

T 1 T * = 0,6089

Para M a 2 = 1

T 2 T * = 1

Então fazemos:

T 2 T * T 1 T * = T 2 T 1 = 1 0,6089

Passo 3

É só achar T 1 que a gente pode calcular T 2 :

T 01 = T 1 1 + k - 1 2   M a 1     2  

Isolando T 1 :

T 1 = T 01 1 + k - 1 2   M a 1     2  

Para o ar k = 1,4 :

T 1 = 600 1 + 1,4 - 1 2   1,8 2 = 364,1   K

Voltando a:

T 2 = 364,1 0,6089 = 598   K

T 2 = 598   K

Resposta

T 2 = 598   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento permanente da água em um canal inclinado para baixo de seção transversal retangular. Se o escoamento é subcrítico e a profundidade do escoamento émenor do que a profundidade nor
É possível que o escoamento subcrítico sofra um salto hidráulico? Explique.
13-72C Por que o salto hidráulico às vezes é usado para dissipar a energia mecânica? Como é definida a taxa de dissipação de energia de um salto hidráulico?
Considere o escoamento permanente da água em um canal inclinado para cima de seção transversal retangular. Se o escoamento é supercrítico, a profundidade do escoamento (a)aumentará, (b) permanecerá co
Água escoa de modo uniforme em um canal retangular com superfícies de concreto polido. A largura do canal é 3 m, a profundidade do escoamento é 1,2 m e a inclinação do fundo é0,002. Determine se o can