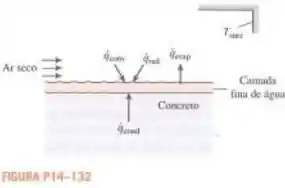
Considere uma fina camada de água líquida em uma superfície de concreto. O ar circundante é seco com coeficiente de transferência de calor por convecção de . A água tem emissividade , e as temperaturas do ar e do ambiente circundante são . Considerando que a camada de água tem temperatura uniforme de , determine o fluxo de calor da condução através do concreto.

Para resolver essa questão, vamos começar encontrando as propriedades devido às condições de baixo fluxo de massa. Podemos usar propriedades de ar seco para a mistura à temperatura média. Temos que a temperatura média é:

As propriedades do ar seco a e são encontradas na Tabela A-15.

Calor específico:

Densidade:

Difusividade térmica:

Também vamos encontrar as propriedades da água a na Tabela A-9.

Densidade da água:

Entalpia de vaporização: .

Vamos precisar também do coeficiente de difusão para uma mistura binária vapor de água no ar a encontrado na Tabela 14-4.

Para determinar o fluxo de calor da condução através do concreto, podemos começar aplicando a analogia de Chilton-Colburn, a fim de obter o coeficiente de transferência de massa. Assim temos:

Aqui, é coeficiente de transferência de massa, é coeficiente médio de transferência de calor, é a densidade do ar é o calor específico do ar, é a difusividade térmica do ar e é coeficiente de difusão para uma mistura binária.

Substituindo os termos da equação pelos dados obtidos, temos:

Agora, vamos calcular a taxa de evaporação por unidade de área usando a seguinte relação:

Aqui, é a taxa de evaporação por unidade de área, é a taxa de evaporação, é a área da superfície da esponja, é a densidades do vapor de água na interface líquido-gás e é a densidade do vapor de água longe da superfície. Temos que para o fluxo de ar seco, a densidade do vapor de água na corrente livre é insignificante .

Substituindo os termos da equação pelos dados obtidos, temos:

Então, o fluxo de calor para cada processo de transferência de calor é:

Evaporação:

Substituindo os termos da equação pelos dados obtidos, temos:

Convecção:

Substituindo os termos da equação pelos dados obtidos, temos:

Radiação:

Substituindo os termos da equação pelos dados obtidos, temos:

Para encontrar o fluxo de calor da condução através do concreto, vamos realizar agora, um balanço energético na camada de água líquida, considerando os processos de evaporação, convecção, radiação e condução. Assim temos:

Substituindo os termos da equação pelos dados obtidos, temos:

Portanto o fluxo de calor da condução através do concreto é .

O valor positivo do fluxo de calor de condução através do concreto indica que o fluxo de calor por condução está entrando na camada de água líquida.