Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 6.Problemas - Ex. 21
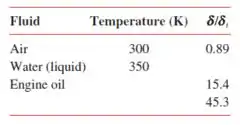
Considere o fluxo da camada limite laminar sobre uma placa plana. Para condições de fluxo idênticas, determine os vapores que não estão mostrados na tabela abaixo, usando o fato de que . A pressão é para cada caso. Dica: Veja os Apêndices A.4 a A.6.
Passo 1
Vamos usar a equação dada no enunciado para cada um dos valores da tabela. Pelo texto do livro, na maioria das vezes tem o valor , vamos usar esse valor na equação:
Para cada fluido, a tabela dá ou a temperatura ou o valor da razão , vamos usar os apêndices que foram dados na dica para completarmos os espaços que faltam.
Passo 2
Na primeira linha já tem os valores para o ar então não precisamos calcular nada, vamos seguir para a água liquida A tabela tem só a temperatura, então pegamos o valor de relativo a essa temperatura usando o apêndice A-6, que é e substituímos na equação:
Passo 3
Agora repetimos o processo para o óleo, a diferença é que nesse caso a tabela dá o valor da razão e não da temperatura, então a gente usa isso para encontrar o número de Prandtl , e depois procuramos o valor correspondente de temperatura. No primeiro caso:
Usando o apêndice A-5, a temperatura que corresponde a esse número é:
E depois encontramos o segundo valor para o óleo:
Que poderia ser algo em torno de:
Isso porque o valor correspondente para esse está entre e peo apêndice, mas como não sabemos como é a dependência da temperatura em reação a fazemos apenas uma estimativa grosseira