Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 14.Problemas - Ex. 116

Considere uma gota de chuva de 3 mm de diâmetro caindo livremente no ar atmosférico, a 25°C. Tomando a temperatura da gota de chuva como sendo 9°C, determine a velocidade terminal da gota de chuva na qual a força de arrasto iguala o peso da gota e o coeficiente médio de transferência de massa naquele momento.

Passo 1

Temos uma gota esférica de diâmetro D = 3   m m caindo em ar atmosférico. A temperatura da gota é T = 9 ° C = 282   K . Devemos determinar a velocidade terminal e o coeficiente de transferência de massa para o processo. Vamos lá???

Passo 2

Vamos começar com o balanço das forças que agem sobre a gota:

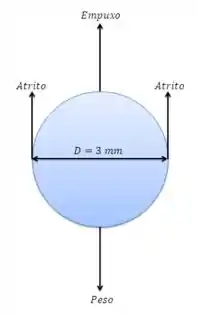
Quando a gota atinge velocidade terminal as forças estão em equilíbrio. Então:

F f + F e = F P

F f = F P - F e

F f = ρ p - ρ f g V p

A densidade da água a 9°C é:

ρ p = 999,74   k g / m 3

A densidade do ar atmosférico a 25°C é:

ρ f = 1 , 184   k g / m 3

ϑ = 1,562 x 10 - 5   m 2 / s

A força de atrito para este caso é:

F f = ρ p - ρ f g V p

F f = 999,74 - 1,184 x 9,81 x π D 3 6

F f = 1,38 x 10 - 4   N

A força de atrito pode ser escrita como:

F f = f A ρ f V 2 2

Para escoamento laminar f = 24 / R e . Então:

F f = 24 ϑ V D x π D 2 4 x ρ f V 2 2

F f = 3 ϑ π D ρ f V

V = F f 3 ϑ π D ρ f

V = 1,38 x 10 - 4 3 x 1,562 x 10 - 5 x π x 0,003 x 1,184

V = 264,8   m / s

Passo 3

Vamos agora determinar o coeficiente de atrito. Como dissemos:

f = 24 / R e

f = 24 ϑ V D

f = 0,000472

Utilizando a analogia de Chilton-Colburn iremos determinar o coeficiente de transferência de massa. Ela é dada por:

f 2 = S t m a s s a S c 2 3

f 2 = h m a s s a ϑ D A B D A B ϑ 2 3

f 2 = h m a s s a ϑ D A B 1 3

h m a s s a = f 2 x D A B ϑ 1 3

A difusividade da água no ar a 25°C e 1 atm é D A B = 2,5 x 10 - 5   m 2 / s . Então:

h m a s s a = 0,000472 2 x 2,5 x 10 - 5 1,562 x 10 - 5 1 3

h m a s s a = 0,000276   m / s

Resposta

A velocidade terminal é V = 264,8   m / s e o coeficiente de transferência de massa é de h m a s s a = 0,000276   m / s .

Ver Outros Exercícios desse livro