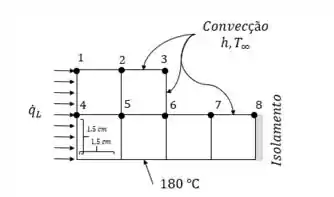
Considere uma transferência de calor permanente bidimensional em um corpo sólido na forma de e a seção transversal dada na Fig. P5–71. A condutividade térmica do corpo é , e o calor é gerado no corpo a uma taxa de . A superfície direita do corpo é isolada, e a superfície inferior é mantida a uma temperatura uniforme de . A totalidade da superfície superior é submetida à convecção para o ar ambiente a , com coeficiente de transferência de calor , e a superfície da esquerda é submetida ao fluxo de calor a uma taxa uniforme de . A rede nodal do problema consiste de 13 nós igualmente espaçados com . Cinco dos nós estão na superfície inferior, portanto suas temperaturas são conhecidas. Obtenha as equações de diferenças finitas dos oito nós restantes e determine as temperaturas nodais resolvendo essas equações.

Aplicando o balanço de energia nos nós temos as seguintes equações de diferenças finitas...

:

:

:

:

:

:

:

: