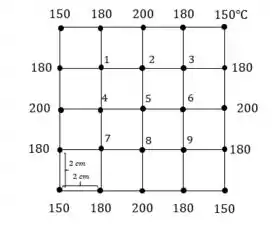
Considere uma transferência de calor permanente bidimensional em um corpo sólido longo cuja seção transversal é dada na Fig. P5–53. As temperaturas medidas nos pontos selecionados da superfície externa são mostradas. A condutividade térmica do corpo é , e não há geração de calor. Usando o método de diferenças finitas com tamanho da malha de , determine as temperaturas do meio nos pontos indicados.

Dica: tire proveito da simetria.

Note que como se trata de uma geometria simétrica, temos que as temperaturas nos seguintes pontos nodais são iguais:

Muito bem!! Isso quer dizer que só precisamos aplicar a equação nos seguintes nós...

:

:

: