Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 65

Considere uma transferência de calor permanente bidimensional em uma longa barra sólida de seção transversal quadrada, na qual o calor é gerado uniformemente a uma taxa de e ˙ = 1,97 × 10 5 W m 3 . A seção transversal da barra tem 16   c m × 16   c m de tamanho, e a condutividade térmica é   k = 28 W m ∙ K . Todos os quatro lados da barra estão sujeitos à convecção com o ar ambiente a T ∞ = 20   ° C , com coeficiente de transferência de calor h = 45 W m 2 ∙ K . Usando o método de diferença finita com malha de ∆ x = ∆ y = 8   c m , determine ( a ) a temperatura dos 9 nós e ( b ) a taxa de perda de calor da barra através da seção de 1   m   de comprimento.

Passo 1

Como primeiro passo vamos anotar os dados do enunciado aqui abaixo:

e ˙ = 1,97 × 10 5 W m 3 ;   k = 28 W m ∙ K ;   h = 45 W m 2 ∙ K ;   ∆ x = ∆ y = 8   c m ;   T ∞ = 20   ° C    

Note que iremos usar nossa equação para malha quadrada:

T s u p + T e s q + T i n f + T d i r - 4 T n ó + e ˙ n ó l 2 k = 0

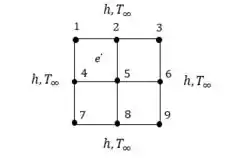
A partir da nossa geometria abaixo...

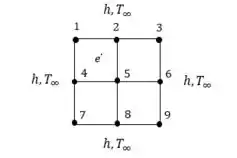
Por simetria podemos considerar T 1 = T 3 = T 7 = T 9 e T 2 = T 4 = T 6 = T 8 . Logo nós iremos precisar apenas de 3 equações para resolvermos.

Passo 2

Muito bem!! Aplicando nossa equação nos nós...

N ó   1 :

2 k l 2 T 2 - T 1 l + 2 h l 2 T ∞ - T 1 + e ˙ 0 l 2 4 = 0

N ó   2 :

2 k l 2 T 1 - T 2 l + k l T 5 - T 2 l + k l T ∞ - T 2 + e ˙ 0 l 2 4 = 0

N ó   5 :

4 T 2 - 4 T 5 + e ˙ l 2 k = 0

Passo 3

Resolvendo as 3 equações simultaneamente, as temperaturas são:

T 1 = T 3 = T 7 = T 9 = 183,37 ° C

T 2 = T 4 = T 6 = T 8 = 193 ° C

T 5 = 203,3 ° C

Passo 4

Logo, para encontrarmos a taxa de perda de calor da barra através da seção de 1   m :

Q ˙ = 8 × Q ˙ ( 1   m   s e ç ã o ,   c o n v ) = 8 × h l 2 T 1 - T ∞ + h l 2 T 2 - T ∞ 1   m = 8 × h l 2 ( T 1 + T 2 - 2 T ∞ ) ( 1   m )

Q ˙ = 5043   W

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro