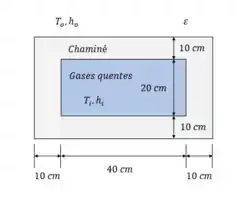
Gases quentes de combustão do forno escoam através de uma chaminé́ de concreto de seção transversal retangular. A seção da chaminé́ é de, e a espessura da parede é de . A temperatura média dos gases quentes na chaminé́ é , e o coeficiente médio de transferência de calor por convecção no interior da chaminé́ é . A chaminé́ perde calor a partir da superfície externa para o ar ambiente a por convecção, com coeficiente de transferência de calor de , e para o céu por radiação. A emissividade da superfície externa da parede é, e a temperatura efetiva do céu é estimada em . Utilizando o método das diferenças finitas com e aproveitando da simetria, obtenha a formulação de diferenças finitas deste problema para transferência de calor permanente bidimensional, determine as temperaturas dos pontos nodais da seção transversal e avalie a taxa de perda de calor para seção de de comprimento da chaminé́.
Dados:
Passo 1
Do enunciado nós temos que:
Nesse exercício há a possibilidade simplifica-lo usando sua simetria. Podemos analisar somente um quarto da geometria, onde a rede nodal terá 10 nós igualmente espaçados:
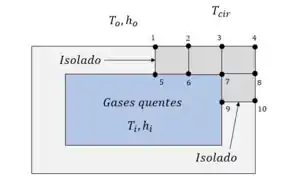
Logo, nenhum calor pode cruzar a linha de simetria sendo tratadas como superfícies isoladas.
Passo 2
Aplicando o balanço de energia em cada ponto nodal temos:
:
:
:
:
:
:
:
:
:
:
Passo 3
Após a resolução das equações simultaneamente, teremos:
Passo 4
Para determinarmos a taxa de transferência de calor, basta aplicarmos essa equação abaixo, lembrando que temos que multiplicar por 4, pois pegamos apenas um quarto da nossa geometria.
Resposta
Ei, a resposta está no passo a passo :)