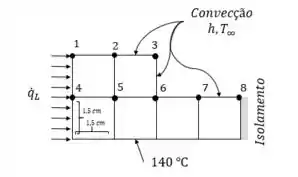
Considere a transferência de calor transiente bidimensional de uma barra sólida em forma de inicialmente a uma temperatura uniforme de , cuja seção transversal é dada na Fig. P5–99. A condutividade térmica e a difusividade do corpo são e respectivamente, e o calor é gerado no corpo a uma taxa de . A superfície da direita do corpo é isolada, e a do inferior é mantida a uma temperatura uniforme de . No momento , toda a superfície superior é submetida à convecção para o ar ambiente a, com coeficiente de transferência de calor, e a superfície da esquerda é submetida a um fluxo de calor uniforme a uma taxa de . A rede nodal dos problemas consiste de 13 nós igualmente espaçados com. Utilizando o método explícito, determine a temperatura no canto superior (nó 3) do corpo após e .

Aplicando o balanço de energia nos nós...

:

:

:

:

:

:

:

Aplicando o critério de estabilidade para obtermos o passo de tempo :

Note que...

Logo temos:

Portanto deve ser escolhido um passo de tempo menor que . Sendo assim vamos escolher um passo de tempo de .

Resolvendo as equações com um auxílio de um computador para 2, 5 e 30 min encontraremos as temperaturas para nó 3 de , e respectivamente.