Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 92

Considere a condução de calor transiente unidimensional em uma parede plana composta de duas camadas A e B   com perfeito contato na interface. A parede não envolve geração de calor e, inicialmente, está em uma temperatura especificada. A rede nodal do meio consiste dos nós 0, 1 (na interface) e 2, com espaçamento nodal uniforme de ∆ x . Usando a abordagem do balanço de energia, obtenha a formulação explícita de diferenças finitas deste problema para o caso de isolamento no nó de contorno da esquerda (nó 0) e de radiação no contorno da direita (nó 2), com emissividade de ε e temperatura do meio envolvente de T c i r .

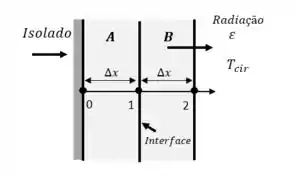
Passo 1

Iremos utilizar o balanço de energia com A = 1 , note que no nó 0 a parede se encontra isolada, e no nó 2 a parede tem ocorrência de radiação.

Além disso há dois tipos de materiais, um material A e um B , na qual seus coeficientes de condutividade térmica serão, k A e k B respectivamente.

Passo 2

Aplicando o balanço de energia...

N ó   0 :

k A T 1 i - T 0 i ∆ x = ρ A ∆ x 2 c p , A T 0 i + 1 - T 0 i ∆ t  

N ó   1 :

k A T 0 i - T 1 i ∆ x + k B T 2 i - T 1 i ∆ x = ρ A ∆ x 2 c p , A + ρ B ∆ x 2 c B T 1 i + 1 - T 1 i ∆ t

N ó   2 :

ε σ T c i r 4 - T 2 i 4 + k B T 1 i - T 2 i ∆ x = ρ B ∆ x 2 c p , B T 2 i + 1 - T 2 i ∆ t

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro