Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 14.Problemas - Ex. 68
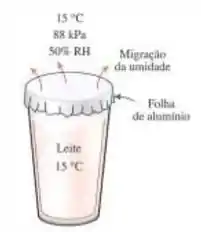
Um copo de leite deixado em cima de um balcão da cozinha a 15°C, 88 kPa e 50% de umidade relativa é hermeticamente fechado por uma folha de alumínio de 0,009 mm de espessura cuja permeação é de . O diâmetro interno do copo é de 12 cm. Supondo que o ar no copo esteja saturado o tempo todo, determine quanto o nível de leite no copo diminuirá em 12 h.
Passo 1
Vamos começar mais uma questão seeensacional!!
Emocionados? Eu estou suuper!!
Nós queremos a quantidade de vapor de água que flui através da superfície de alumínio ao longo de um período de tempo, o que nós vamos precisar achar ?
A vazão mássica do vapor, não é?
Bora ver a fórmula?
Sabemos que a permeabilidade pode ser dada como:
Onde M é a permeação e L a espessura!
Então:
Reorganizando:
O que sabemos?
Ixiii!!
Vamos ver o que mais podemos descobrir?
A área é molezinha, já que temos uma seção circular:
Se:
Então:
Passo 2
Agora nós precisamos da pressão de vapor, certo?
Quando a temperatura e a umidade relativa são conhecidas, a pressão do vapor é calculada como:
Quando:
Lembrando que no copo o ar está saturado:
Agora podemos achar a pressão de vapor:
Com isso nós podemos achar a vazão mássica:
Acabamos?
Que nada né!
Passo 3
Nós achamos a vazão mássica mas o que nós queremos realmente é o volume perdido junto com essa massa, certo?
Se usarmos a densidade podemos relacionar a massa e o volume:
Sabemos que para a água:
Se nós queremos a massa após um período de 12 h vamos precisar usar a seguinte fórmula:
Vamos substituir?
Colocando na fórmula do volume:
Em mL:
Sendo assim, o copo perdera ao longo destas 12 h, de leite !!
Gostaram?