Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 31
Se, com os dados do exercício anterior, ocorrer uma onda de choque normal numa seção de área determinar:
- As propriedades de estagnação na seção de saída do divergente;
- A variação de velocidade entre a entrada e a saída da onda choque;
- A vazão em massa
Passo 1
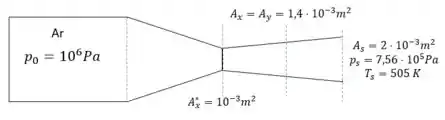
Item a)
Para calcular as propriedades de estagnação na seção de saída do divergente precisaremos da área crítica à jusante . Mas para calculá-la vamos precisar fazer um longo caminho pelas tabelas, acompanhe:
Vamos utilizar as relações entre a área crítica e a área do ponto de choque para determinar as propriedades à montante
Utilizando o número de Mach podemos usar a tabela 2 para encontrar o número de Mach à jusante
Agora possuímos o e podemos usá-lo para determinar a razão entre a área crítica e a área do ponto de choque à jusante.
Vamos determinar à área crítica para o escoamento à jusante
Agora vamos relacionar a área de saída com a área crítica à jusante para podemos determinar as propriedades de estagnação na saída:
Agora podemos determinar as propriedades de estagnação na saída:
Passo 2
Vamos pegar nas tabelas outras propriedades importantes para resolução da questão:
Passo 3
Item b)
Para calcular as velocidades, primeiro precisamos calcular as temperaturas a montante e a jusante. Vale lembrar que a temperatura crítica é igual em todo o escoamento.
A velocidade à imediatamente à jusante do ponto de choque é:
A diferença entre as velocidades é:
Passo 4
Item C) Para determinar a vazão mássica vamos usar a equação:
Vamos usar a lei dos gases para determinar a densidade na saída:
A velocidade na saída pode ser determinada também:
Agora, basta aplicar a equação da vazão:
Resposta
- ; ;