Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 35

É dado um bocal convergente/divergente alimentado pelo reservatório da figura. Para uma certa pressão de jusante, a vazão em massa é máxima, a temperatura na seção (1) é 373 K e o escoamento é contínuo em todo o divergente. Modificando as condições a jusante, observa-se uma onda de choque na seção (1). Determinar a diferença de temperatura entre os pontos imediatamente a jusante a montante da onda de choque e esquematizar a variação de pressão ao longo do bocal para as duas condições de jusante ( k = 1,4 ; R = 287   m 2 / s 2 K ) .

Passo 1

Vamos pensar na situação 1, onde a vazão mássica é a maior possível e o escoamento é subsônico

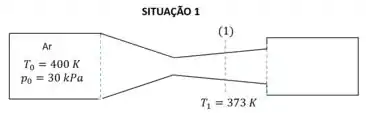
Usando a tabela 1 poderemos relacionar á área do ponto (1) com a área crítica da garganta

T 1 T 0 = 373 400 = 0,9326 ⇒ T a b e l a   1 A 1 A * = 1,188 M 1 = 0,6

Passo 2

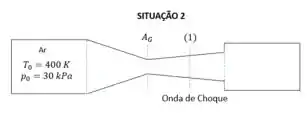
Agora vamos pensar na segunda situação, onde ocorre uma onda de choque no ponto (1), ou seja o escoamento é supersônico. Vamos usar a realção de área para pegar na Tabela 1 os dados para um escoamento supersônico e determinarmos a temperatura à montante

A 1 A * = 1,188 ⇒ T a b e l a   1 T X T 0 = 0,648 M x = 1,52

T X T 0 = 0,684 ⇒ T x = 0,684 ⋅ T 0 = 0,684 ⋅ 400 ⇒ T x = 273,6   K

Com o valor do número de Mach podemos utilizar a tabela 2 para calcular a temperatura à jusante

M X = 1,52 ⇒ T a b e l a   2   T y T x = 1,333

T y T x = 1,333 ⇒ T y = 1,333 ⋅ T x = 1,333 ⋅ 274 ⇒ T y = 365,24   K

Passo 3

A diferença entre temperaturas é:

Δ T = T y - T x

Δ T = 365,24   - 273,6  

Δ T = 91,64   K

Resposta

Δ T = 91,64   K

Ver Outros Exercícios desse livro