Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 108
Os dados na Figura P7.108 referem-se a sustentação e arrasto de uma esfera girante da Referência 45. Admita que uma bola de tênis (P = 0,56 N, D = 6,35 cm) seja golpeada ao nível de mar com velocidade inicial V0 = 30 m/s, com efeito topspin (frente da bola girando para baixo) de 120 rps. Se a altura inicial da bola for 1,5 m, calcule a distância horizontal percorrida antes que ela atinja o solo.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, temos uma bola girando a uma velocidade angular de . Ela parte de uma altura inicial de a uma velocidade . A bola tem peso e diâmetro .
Vamos considerar que essa bola descreve uma seção circular de ângulo e raio , que pode ser enxergada no esquema abaixo que fizemos pra te orientar:
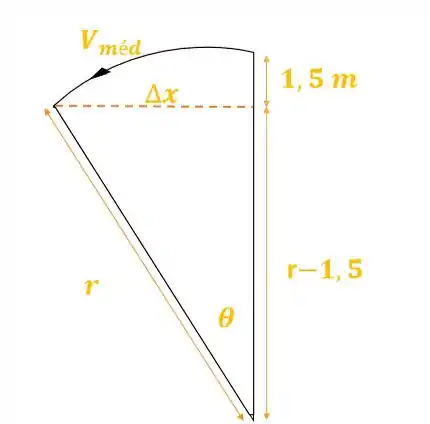
Sendo a velocidade média da bola indo de até o momento que ela cai no chão.
O enunciado nos pede pra calcular a distância horizontal percorrida por essa bola, e pra isso nós vamos usar suas forças de arrasto e sustentação.
Antes de irmos para os próximos passos, temos que lembrar que as propriedades do ar a temperatura ambiente são e .
Então vem comigo pra gente resolver esse problema juntos!
Passo 2
Pra resolver o problema, devemos ir na Figura P7.108 pra calcular os coeficientes de arrasto e sustentação pra bola em movimento.
Pra isso, vamos calcular o valor pro termo de entrada :
Agora entramos com esse valor no gráfico da Figura P7.108:
Dessa maneira, encontramos um coeficiente de arrasto e outro de sustentação de, respectivamente, e .
Vamos então calcular as forças de arrasto e de sustentação com base na velocidade inicial :
Passo 3
Agora, vamos calcular as desacelerações horizontal e vertical dessa bola.
A desaceleração horizontal será basicamente dada pela força de arrasto, a que age na direção horizontal:
Já a desaceleração vertical , causada pela força de sustentação, também levará em conta a gravidade agindo no sistema:
Passo 4
Nesse passo, vamos finalizar a questão.
Vamos usar pra calcular a velocidade na qual a bola toca o chão, que ocorre a aproximadamente . Sendo assim, sua velocidade final é aproximadamente de .
Portanto, nossa velocidade média será . Com ela e com aceleração vertical podemos encontrar o raio da seção circular percorrida pela bola:
Agora dê uma olhada na figura exposta no Passo 1. Pra achar o ângulo da seção circular, basta usar fazendo uma simples relação trigonométrica:
E uma relação trigonométrica similar pode ser usada pra encontrar a distância horizontal :
Pronto, matamos a questão juntos!
Resposta
A distância horizontal percorrida antes que a bola atinja o solo é