Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 12.Problemas - Ex. 39

Deduza novamente a equação para a velocidade do som (Eq. 12.18), considerando que o sentido do movimento do fluido atrás da onda de som é d V x para a direita. Mostre que o resultado é idêntico ao dado pela Eq. 12.18.

Passo 1

Oi pessoal, tudo bem?

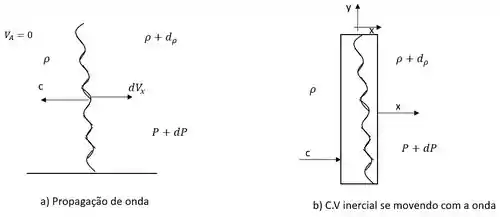
Temos o nosso esboço para começar a dedução para a velocidade do som.

Por continuidade, temos:

0 = - ρ c A + ρ d ρ c + d V A         →       0 = - ρ c A + ρ c A + ρ d V x A + c A d ρ + d ρ d V x

Cancelando termos opostos, têm-se:

ρ d V x + c d P = 0       o u       d V x = - c ρ d ρ   ( 1 )

Ao aplicar a equação do momento x ao mesmo c.v dá:

∑ F S x = P A - P x d P A = ∫ V x ρ V x , y , z → d A = c - ρ A c + c + d V x ρ A c - A d P = ρ A c   d V x  

Então:

d V X = - d P ρ c   ( 2 )

Combinando as equações 1 e 2 nós obtemos:

c 2 = d P d ρ  

Resposta

Este é o mesmo resultado obtido na derivação de com a direção do movimento do fluido atrás da onda para a esquerda

Ver Outros Exercícios desse livro