Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 2.Problemas - Ex. 8
A densidade do ar atmosférico varia com a altitude, diminuindo com o aumento da altitude. (a) Usando os dados da tabela, obtenha a relação da variação da densidade com a altitude e calcule a densidade na altitude de 7000 m. (b) Calcule a massa da atmosfera usando a correlação que você obteve. Suponha que a Terra seja uma esfera perfeita com raio de 637 km e considere que a espessura da atmosfera seja 25 km.
Passo 1
Oi pessoal, tudo bem?
Bem, assumimos inicialmente que:
1. O ar atmosférico se comporta como um gás ideal.
2. A terra é perfeitamente esférica com um raio de 6377 km no nível do mar, e a espessura da atmosfera é de 25 km.
Então, devemos encontrar uma equação característica para a tabela dada no problema, que relaciona a altitude com a densidade do ar atmosférico. Para isso, vamos utilizar o software EES.
Passo 2
Letra a) Primeiramente, admitimos que o raio km, em que representa a altitude. Inserindo essa relação encontramos uma tabela parecida com a mostrada no problema:
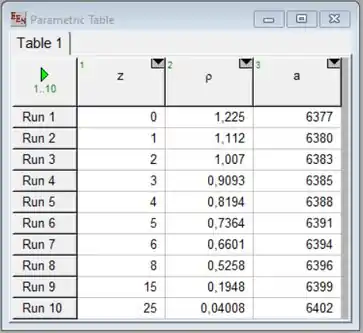
Onde: é dado em .
Passo 3
A partir da tabela encontrada, podemos gerar um gráfico que relaciona a altitude com a densidade do ar :
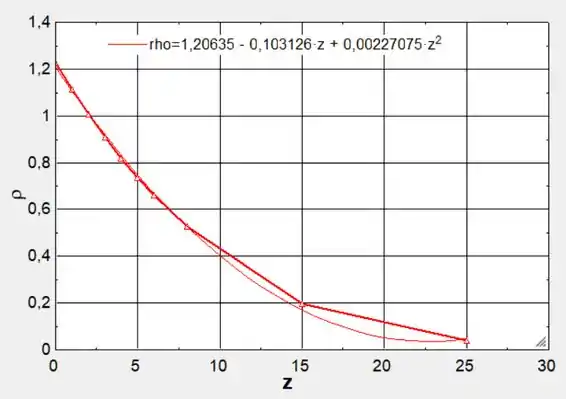
É possível perceber também que, utilizando uma ferramenta do EES, podemos achar uma equação do segundo grau (curva) característica para tal problema.
Portanto, substituindo o e resolvendo a equação do segundo grau encontrada, temos que:
Para
Passo 4
Letra b) A massa da atmosfera pode ser encontrada como:
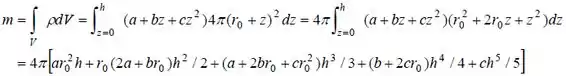
Onde = 6377 km é o raio da terra, h = 25 km é a espessura da atmosfera. Além disso, a = 1,20252, b = -0,101674 e c = 0,0022375 são as constantes na função de densidade mostrada no gráfico da curva característica encontrada para essa relação.
Substituindo e multiplicando pelo fator para converter a densidade de unidades de em , a massa da atmosfera é determinada em aproximadamente:
Resposta
Portanto:
Letra a)
Letra b)