Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 15.Problemas - Ex. 26
Desenhe novamente a malha multiblocos estruturada da Figura 5-12b para o caso no qual seu código CFD pode processar apenas blocos elementares. Renumere todos os blocos e indique quantos intervalos e estão contidos em cada bloco. Com quantos blocos elementares você fica? Some todas as células e verifique se o número total de células não mudou.
Passo 1
Fala aí, galerinha. Tudo beleza? Vamos fazer mais uma questão de MecFlu pra tirar aquele na prova. Neste problema devemos gerar soluções CFD para fluxo externo em um bloco . Especificamente, devemos comparar o arrasto coeficiente para vários valores de (a extensão do limite externo do domínio computacional). Além disso, devemos comparar o valor calculado de com o experimento.
Primeiro, temos que o fluxo é bidimensional e incompressível, além de ser simétrico em relação ao eixo . O escoamento é turbulento, mas constante na média. Dado que e, temos que o número Reynolds é:
Estes dados experimentais indicam que o coeficiente de arrasto para este corpo é em números de Reynolds maiores que .
Passo 2
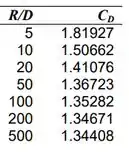
Sabemos que o código CFD é executado para oito valores de , todos os outros sendo iguais. Temos que é tabulado como uma função de . Temos:
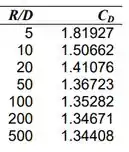
Podemos plotar estes dados. Fica assim:
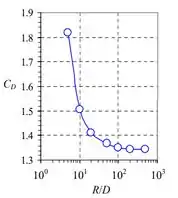
Temos que à medida que a extensão do domínio computacional cresce em tamanho, o coeficiente de arrasto diminui continuamente, mas se estabiliza em três dígitos significativos de precisão de . Assim, uma extensão do domínio computacional de é suficiente para alcançar a independência de .Logo:
Passo 3
Agora vamos discutir as várias razões possíveis para a discrepância entre o valor calculado de e o valor obtido experimentalmente de .
Em primeiro lugar, o fluxo real é provavelmente instável, com vórtices sendo lançados na esteira, enquanto estamos simulando um fluxo constante. Além disso, o derramamento instável de vórtices torna o fluxo não mais simétrico em relação ao eixo , enquanto estamos forçando nosso fluxo a ser simétrico. Além disso, a resolução da rede pode não ser adequada para alcançar a sua independência.
Finalmente (e mais importante), estamos usando um modelo de turbulência para simular este campo de fluxo. A solução CFD que obtemos é tão boa quanto o grau em que o modelo de turbulência modela corretamente a física da turbulência. Ou seja, nenhum modelo de turbulência é universalmente válido para todos os tipos de fluxos turbulentos. As discrepâncias entre o experimento e o CFD sempre existirão, independentemente de quão fina seja a grade ou quão grande seja a extensão do domínio computacional.
Passo 4
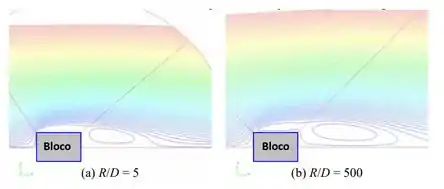
Por fim, sabemos que linhas de corrente perto do corpo são plotadas para e :
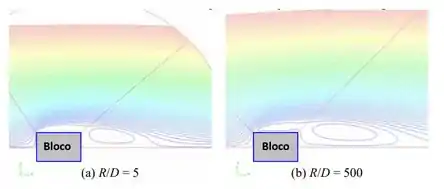
Notamos que as linhas de fluxo para o caso são mais estreitas ao redor do corpo em comparação com aquelas para Isso é provavelmente devido à interferência das bordas externas do domínio computacional, que são muito próximas para o caso .
É isso, galera. Bora pra praticar mais pra ficar craque.
Resposta
