Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 14.Problemas - Ex. 32

Determine a fração molar do vapor de água na superfície de um lago cuja temperatura na superfície é de 21°C e compare com a fração molar da água no lago. Considere a pressão atmosférica no nível do lago de 95 kPa.

Passo 1

Animados para mais uma??

Espero que siiim !!

Bom galera, nesta situação nós temos ar saturado na superfície do lago e entre o ar e esta superfície existe uma interface ar-água, olhem só esse desenho:

No lado do ar nós teremos uma certa fração molar de vapor de água, enquanto o lago será composto de água, em sua grande maioria, e ar. Estamos tranquilos até aqui?

Então beleza !!

Vamos começar calculando a a fração molar do vapor de água no ar, certo?

Se nós considerarmos que o ar e o vapor de água são gases ideais nós poderemos calcular a fração molar como:

y v a p o r = P v a p o r P = P s a t P a t m

Olhando a Tabela A-9, quando a temperatura é 21°C nós vamos ter que fazer a interpolação:

P s a t = P s a t ,   T 1 + T - T 1 P s a t ,   T 2 - P s a t ,   T 1 T 2 - T 1

Usando:

T 1 = 20 ° C →   P s a t ,   T 1 = 2,339

T 2 = 2 5 ° C →   P s a t ,   T 2 = 3,169

Substituindo:

P s a t = 2,339 + 21 ° C - 20 ° C 3,169 - 2,339 25 ° C - 20 ° C

P s a t = 2,505   k P a

Então galerinha nós já temos tudo que precisamos:

P v a p o r = P s a t = 2,505   k P a

P = 9 5   k P a

Agora é só nós substituirmos:

y v a p o r = 2,505   k P a 9 5   k P a

y v a p o r = 0,0 264

Então nós temos uma fração molar de vapor de 0,0264 no ar saturado !

Passo 2

Agora nós vamos calcular qual a fração molar de água no lago, sabendo que:

y H 2 O = 1 - y a r - á g u a

Só precisamos calcular a fração do ar, certo?

Para calcular a fração molar do ar no líquido podemos usar a Lei de Henry, se lembram?

Se não lembram não tem problema, eu mostro pra vocês:

y a r _ á g u a = P a r H

Bom, nossa pressão total é de 95 kPa apenas 2,505 kPa é devido ao vapor de água, então o que sobra é a pressão causada pelo ar, ok?

P a r = P - P v a p o r

Substituindo:

P a r = 9 5   k P a - 2,505   k P a

P a r = 92,495   k P a

E quanto a constante de Henry? Vamos olhar a tabela:

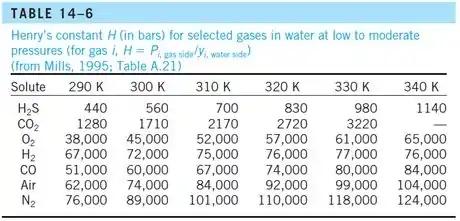
Já vimos que precisamos da temperatura em kelvin, então:

T = 21 ° C + 273 = 2 94   K

Maaais uma interpolação?

H T = H   T 1 + T - T 1 H   T 2 - H   T 1 T 2 - T 1

Usando:

T 1 = 290   K →   H   T 1 = 62000

T 2 = 300   K →   H ,   T 2 = 74000

Substituindo:

H T = 62000 + 294   K - 290 K 74000 - 62000 300 K - 290 K

H T = 66800   b a r

Transformando em kPa:

H = 66800   b a r × 100   k P a 1   b a r = 6 68 0000   k P a

E agora que temos tudo só precisamos substituir:

y a r _ á g u a = 92,495   k P a 6680000   k P a

y a r _ á g u a = 1 , 3847 × 10 - 5

Era isso que queríamos?

Que nada né, nós precisamos da fração da água no lago!

Então é só substituir na primeira equação:

y H 2 O = 1 - 1,3847 × 10 - 5

y H 2 O = 0,9999

Se formos comparar nós vemos que no lago a porcentagem é bem maior do que o vapor no ar saturado, normal não é?

E é só galerinha ! :P

Resposta

A r   S a t u r a d o :   0,0264 ;

L a g o : 0,9999 .

Ver Outros Exercícios desse livro