Dois discos paralelos de diâmetro , separadis por , estão localizados diretamente um acima do outro. Os discos são separados por um escudo de radiação com emissividade de . Ambos os discos são negros, mantidos em temperaturas de e , respectivamente. O ambiente em que os discos estão pode ser considerado um corpo negro a . Determine a taxa líquida da transferência de calor por meio da radiação sob o escudo em condições permanentes.
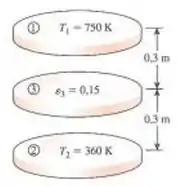
Passo 1
Considerações:
- Superfícies difusas, cinza e opacas;
- Condições estáveis de operação;
- Transferência de calor resumida à radiação.
Passo 2
A partir da figura de fator de visualização entre dois discos paralelos coaxiais:
Assim:
Dados:
;
;
;
;
;
;
;
.
Passo 3
O disco no meio é cercado por superfícies negras pelos dois lados.
A transferência de calor pela superfície superior do disco do meio é dada como:
Substituindo os dados:
Do mesmo modo, a transferência de calor pela superfície inferior do disco do meio é dada como:
Substituindo os dados:
Igualando as duas equações, obtemos:
Passo 4
Substituindo o valor de obtido na equação de transferência de calor pela superfície inferior do disco do meio conseguimos calcular a taxa líquida da transferência de calor: