Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 41

Dois tubos de vapor de ferro fundido k = 52 W m ∙ K ,   ε = 0,8 de 10   c m de diâmetro externo, 3   m de comprimento e 0,4   c m de espessura são conectados entre si por meio de dois flanges de 20   c m de diâmetro externo e 1 cm de espessura, como mostrado na Fig. P5–41. O vapor escoa no interior do tubo a uma temperatura média de 250   ° C , com coeficiente de transferência de calor de 180 W m 2 ∙ K . A superfície externa do tubo está exposta à convecção com o ar ambiente a 12   ° C , com coeficiente de transferência de calor de 25 W m 2 ∙ K , bem como à radiação com as superfícies ao redor a uma temperatura média de T c i r = 290   K . Pressupondo uma condução de calor permanente unidimensional ao longo dos flanges e um espaçamento nodal de 1   c m ao longo do flange, ( a ) obtenha a formulação de diferenças finitas de todos os nós, ( b ) determine a temperatura na ponta do flange resolvendo essas equações e ( c ) determine a taxa de transferência de calor a partir da superfície exposta do flange.

Dados: σ = 5,67 × 10 - 8 W m 2 ∙ K 4

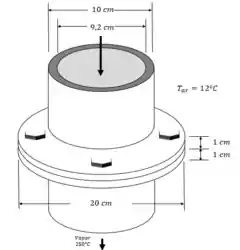
Passo 1

Vamos separar aqui os dados do enunciado:

k = 52 W m ∙ K ;   ε = 0,8 ;   ∆ x 1 = 0,004   m ;   ∆ x 2 = 0,01   m ; T ∞ = 12 ° C ,   T i n t = 250 ° C ; T c i r = 290   K  

t = 0,02   m ;   h o = 25 W m 2 ∙ K ; h i = 180 W m 2 ∙ K ;   σ = 5,67 × 10 - 8 W m 2 ∙ K 4

Passo 2

Precisamos calcular o número de nós para iniciarmos a análise, e podemos fazer isso utilizando a equação abaixo para esse caso:

M = L ∆ x + 2 = 5   c m 1   c m + 2 = 7

Note que estamos utilizando o espaçamento do flange para encontrar o número de nós, porém o espaçamento do nó 0 para o nó 1, será de ∆ x 1 = 0,004   m . Representando:

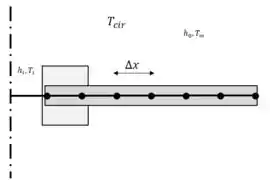
A espessura total do flange é de t = 0,02   m , porém a área de condução de calor A c o n d = 2 π r t , irá variar no raio...

r 0   =   0.046   m ,   r 1 = 0.05   m ,   r 2 = 0.06   m ,   r 3 = 0.07   m ,   r 4 = 0.08   m ,   r 5 = 0.09   m ,   r 6 = 0.10   m

r 01 = 0.048   m ,   r 12 = 0.055   m ,   r 23 = 0.065   m ,   r 34 = 0.075   m ,   r 45 = 0.085   m ,   r 56 = 0.095   m

Passo 3

Muito bem! Agora podemos determinar as nossas 7 equações, ou seja, uma equação para cada nó. Lembrando que temos a presença de radiação!

N ó   0 :

h i 2 π r 0 T i - T 0 + k 2 π t r 01 T 1 - T 0 ∆ x 1 = 0

N ó   1 :

k 2 π t r 01 T 0 - T 1 ∆ x 1 + k 2 π t r 12 T 2 - T 1 ∆ x 2 + 2 2 π t r 1 + r 12 2   ∆ x 2 2 { h T ∞ - T 1 + ε σ [ T c i r 4 - T 1 + 273 4 ) ] } = 0

N ó   2 :

k 2 π t r 12 T 1 - T 2 ∆ x 2 + k 2 π t r 23 T 3 - T 2 ∆ x 2 + 2 ( 2 π t r 2 ∆ x 2 ) { h T ∞ - T 2 + ε σ [ T c i r 4 - T 2 + 273 4 ) ] } = 0

N ó   3 :

k 2 π t r 23 T 2 - T 3 ∆ x 2 + k 2 π t r 34 T 4 - T 3 ∆ x 2 + 2 ( 2 π t r 3 ∆ x 2 ) { h T ∞ - T 3 + ε σ [ T c i r 4 - T 3 + 273 4 ) ] } = 0

N ó   4 :

k 2 π t r 34 T 3 - T 4 ∆ x 2 + k 2 π t r 45 T 5 - T 4 ∆ x 2 + 2 ( 2 π t r 4 ∆ x 2 ) { h T ∞ - T 4 + ε σ [ T c i r 4 - T 4 + 273 4 ) ] } = 0

N ó   5 :

k 2 π t r 45 T 4 - T 5 ∆ x 2 + k 2 π t r 56 T 6 - T 5 ∆ x 2 + 2 ( 2 π t r 5 ∆ x 2 ) { h T ∞ - T 5 + ε σ [ T c i r 4 - T 5 + 273 4 ) ] } = 0

N ó   6 :

k 2 π t r 56 T 5 - T 6 ∆ x 2 + 2 2 π t ∆ x 2 2 r 56 + r 6 2 + 2 π r 6 t { h T ∞ - T 2 + ε σ [ T c i r 4 - T 2 + 273 4 ) ] } = 0

Passo 4

Resolvendo as 7 equações simultaneamente, temos que as temperaturas são:

T 0 = 148,4 ° C

T 1 = 147,0 ° C

T 2 = 144,1 ° C

T 3 = 141,6 ° C

T 4 = 139,5 ° C

T 5 = 137,7 ° C

T 6 = 136,0 ° C

Passo 5

A taxa de transferência de calor pode ser encontrada a partir da equação abaixo:

Q ˙ a l e t a = ∑ m = 1 6 Q ˙ e l e m e n t o ,   m = ∑ m = 1 6 h A s u p e r f í c i e ,   m T m - T ∞ + ∑ m = 1 6 ε σ A s u p e r f í c i e ,   m [ T m + 273 4 - T c i r 4 ]

Q ˙ a l e t a = 105,7   W

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro