Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 50

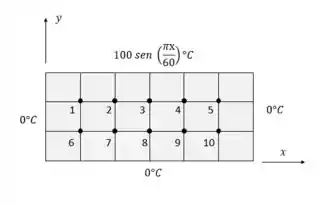
Considere uma transferência de calor constante bidimensional em uma seção transversal retangular ( 60   c m ×   30   c m ) com temperaturas prescritas nas superfícies esquerda, direita e inferior de 0   ° C . A superfície superior é dada como 100 sen ⁡ π x 60 Usando uma malha uniforme ∆ x = ∆ y , determine ( a ) as equações de diferenças finitas e ( b ) as temperaturas nodais.

Passo 1

Muito bem pessoal, note que temos 10 pontos nodais interiores a partir da imagem. Podemos usar nossa equação geral para diferenças finitas abaixo:

T m - 1 , n - 2 T m , n + T m + 1 ,   n ∆ x 2 + T m , n - 1 - 2 T m , n + T m ,   n + 1 ∆ y 2 = 0

Como ∆ x = ∆ y , podemos simplificar essa equação para ficar mais fácil de trabalhar, logo:

T m , n = 0,25 ( T m , n + 1 + T m - 1 , n + T m , n - 1 + T m + 1 , n )

O que podemos interpretar como:

T n ó = 0,25 T s u p + T e s q + T i n f + T d i r

Passo 2

Tendo nossa equação em mãos. Aplicando em cada nó eles ficaram...

N ó   1 :

T 1 = 0,25 100 sen ⁡ π 6 + 0 + T 6 + T 2

N ó   2 :

T 2 = 0,25 100 sen ⁡ 2 π 6 + T 1 + T 7 + T 3

N ó   3 :

T 3 = 0,25 100 sen ⁡ 3 π 6 + T 2 + T 8 + T 4

N ó   4 :

T 4 = 0,25 100 sen ⁡ 4 π 6 + T 3 + T 9 + T 5

N ó   5 :

T 5 = 0,25 100 sen ⁡ 5 π 6 + T 4 + T 10 + 0

N ó   6 :

T 6 = 0,25 T 1 + 0 + 0 + T 7  

N ó   7 :

T 7 = 0,25 T 2 + T 6 + 0 + T 8  

N ó   8 :

T 8 = 0,25 T 3 + T 7 + 0 + T 9  

N ó   9 :

T 9 = 0,25 T 4 + T 8 + 0 + T 10  

N ó   10 :

T 10 = 0,25 T 5 + T 9 + 0 + 0  

Passo 3

Resolvendo as equações simultaneamente, podemos chegar nas seguintes temperaturas:

T 1 = 27,4 ° C

T 2 = 47,4 ° C

T 3 = 54,7 ° C

T 4 = 47,4 ° C

T 5 = 27,4 ° C

T 6 = 12,1 ° C

T 7 = 20,9 ° C

T 8 = 24,1 ° C

T 9 = 20,9 ° C

T 10 = 12,1 ° C

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro