Um duto de aquecimento de ar é constituído por um arranjo alinhado de elementos de aquecimento elétricos no qual os passos longitudinal e transversal são . Há filas de elementos na direção do escoamento e elementos por fila Ar atmosférico com uma velocidade a montante de e uma temperatura de escoa em escoamento cruzado sobre os elementos, que têm um diâmetro de , um comprimento de e são mantidos com uma temperatura superficial de .

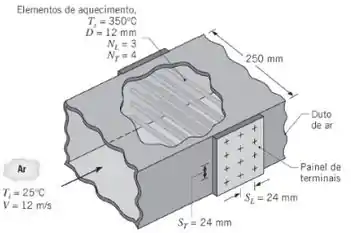
(a) Determine a transferência de calor total para o ar e a temperatura do ar deixando o duto aquecedor.

(b) Determine a queda de pressão ao longo do feixe de elementos e a potência necessária do ventilador.

(c) Compare o coeficiente convectivo médio obtido em sua análise com o valor para um elemento isolado (sozinho). Explique a diferença entre os resultados.

(d) Qual efeito teria o aumento dos passos longitudinal e transversal para na temperatura de saída do ar, na taxa de transferência de calor e na queda de pressão?

Para resolver essa questão vamos assumir que: estamos em condição de estado estacionário, os efeitos da radiação são desprezíveis, o efeito da mudança na temperatura do ar através do banco de tubos nas propriedades do ar é desprezível. As propriedades foram retiradas da Tabela A.4.

Na letra (a) queremos encontrar a transferência de calor total para o ar e a temperatura do ar deixando o duto aquecedor. A transferência total de calor para o ar é determinada a partir da equação da taxa:

Onde a diferença de temperatura média do é:

E do balanço energético geral,

As propriedades e são avaliados à temperatura de entrada . E vamos encontrar o coeficiente de convecção médio usando a correlação de Zukauskus,

Onde são determinados na Tabela 7.5 para a configuração alinhada com e . Todas as propriedades, exceto , são avaliadas à temperatura média aritmética:

O número máximo de Reynolds é:

Onde para o arranjo alinhado, a velocidade máxima ocorre no plano transversal,

Os resultados das análises para estão tabulados abaixo.

Na letra (b) queremos encontrar a queda de pressão ao longo do feixe de elementos e a potência necessária do ventilador. A queda de pressão através do feixe de tubos é:

Onde o fator de atrito, , e o fator de correção, , são determinados na Fig. 7.14 usando .

e

Então,

A energia requisitada pelo ventilador é:

Onde é a vazão volumétrica. Para este cálculo, foi avaliado em

Na letra (c) queremos comparar o coeficiente convectivo médio obtido com o valor para um elemento isolado (sozinho). Para um único elemento no fluxo cruzado, o coeficiente de convecção médio pode ser estimado usando a correlação de Churchill-Bernstein,

Onde todas as propriedades são avaliadas à temperatura do filme, . E os resultados dos cálculos são:

, e

Vamos comparar o elemento isolado, ao valor médio da matriz, ⋅ Como a primeira linha da matriz atua como uma grade de turbulência, o coeficiente de transferência de calor para a segunda e terceira linhas será maior que para a primeira linha. Aqui, o valor da matriz é o dobro do valor para o elemento isolado.

Na letra (d) queremos avaliar qual efeito teria o aumento dos passos longitudinal e transversal para na temperatura de saída do ar, na taxa de transferência de calor e na queda de pressão.

O efeito pode ser explicado pelo reconhecimento de que o número máximo de Reynolds será diminuído, o que resultará em valores mais baixos para o coeficiente de convecção e queda de pressão. Repetindo os cálculos da parte (a) para , encontramos:

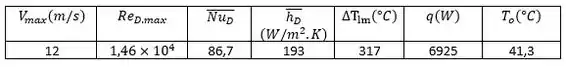
Com a parte (b) para queda de pressão e potência do ventilador, temos:

, e