Enquanto corria na praia (em um dia quente de verão, em torno de 25°C) um jato de alta velocidade sobrevoa. Você estima que a altitude seja em torno de 3000 m, e conta em torno de 7,5 s antes de ouvi-lo. Estime a velocidade e o número de Mach do jato.
Passo 1
Oi pessoal, tudo bem?
Para o esboço do que é descrito no problema, temos:
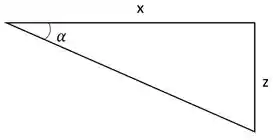
Então, podemos dizer que:
Consideremos:
Obs: Propriedades do ar (Tabela A.6). ;
Passo 2
Sabemos que a velocidade do som:
E que a velocidade do avião depende da velocidade do som, de modo que:
Primeiramente, a velocidade do som:
O problema agora é que não sabemos ainda o número de Mach. Porém temos algumas relações, tais como:
Substituindo o valor de x:
Entretanto, o cone de Mach tem como relação:
Então:
Como , podemos substituir este valor na equação 3:
Passo 3
Então, a equação 2:
Portanto, a velocidade é:
Resposta
Portanto: