Ar entra em um bocal convergente-divergente com velocidade baixa a 2,0 MPa e 100°C. Se a saída de área do bocal for 3,5 vezes a área de garganta, qual é a contrapressão necessária para produzir um choque normal no plano de saída do bocal?
Passo 1
Vamos lá!! O ar entra com velocidade baixa, então a gente pode considerar a velocidade nula e dizer que temos um ponto de estagnação, certo?!
Agora vamos visualizar o que ta acontecendo:
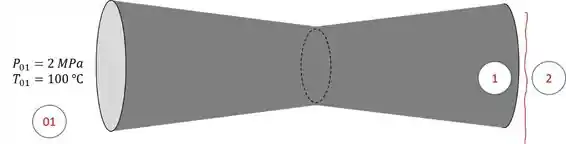
A gente quer a contra pressão, que é , então bora atrás dele!!
Passo 2
O enunciado diz que a área de saída do bocal é vezes maior que a área da garganta, isso é o mesmo que dizer que:
Mas como a gente pode fazer as relações necessárias para responder esse problema?!
Aqui tem um jeito mais fácil do que usar váaarias equações!!
A gente vai correr lá atrás do livro e olhar a tabela , lá a gente enconta váaarias informações importantes, tipo:
Traduzindo para os pontos que a gente escolheu, temos:
Temos e podemos achar !
Passo 3
Sabendo a gente pode olhar uma outra tabela!!
Na tabela a gente acha relações de diversas variáveis quando existe a onda de choque, para a gente acha:
Sabemos então é só substituir e calcular:
Uhuuuul!!