Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 12.Problemas - Ex. 83

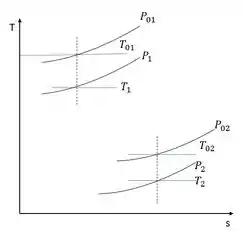
Ar entra em uma turbina a M 1 = 0,4, T 1 = 1250°C e P 1 = 625 kPa (absoluta). As condições na saída da turbina são M 2 = 0,8, T 2 = 650 0 C e P 2 = 20 kPa (absoluta). Avalie as condições locais de estagnação isentrópica (a) na entrada da turbina e (b) na saída da turbina. Calcule a variação na entropia específica através da turbina. Mostre os pontos de estado estático e de estagnação em um diagrama Ts.

Passo 1

Oi pessoal, tudo bem ?

Primeiro, vamos relembrar as equações de estagnação pela razão de pressão e temperatura isentrópica:

P 0 P = 1 + k - 1 2 M 2 k k - 1       e       T 0 T = 1 + k - 1 2 M 2

Consideremos:

  T 1 = 1523   K     T 2 = 923   K     P 1 = 625   k P a     |     P 2 = 20   k P a       M 1 = 0,4       M 2 = 0,8  

Obs: Propriedades do ar (Tabela A.6). R = 286,9 J K g K k = 1,4     c p = 1004 J K g K ;

Passo 2

Para a temperatura de estagnação:

T 01 = 1523 * 1 + 1,4 - 1 2 * 0,4 2             → T 01 = 1572   K

T 02 = 923 * 1 + 1,4 - 1 2 * 0,8 2             → T 02 = 1041   K

A pressão de estagnação pode ser calculada:

P 01 = 625 * 10 3 1 + 1,4 - 1 2 * 0,4 2 1,4 1,4 - 1       → P 01 = 698   k P a

P 02 = 20 * 10 3 1 + 1,4 - 1 2 * 0,8 2 1,4 1,4 - 1       → P 02 = 30   k P a

A alteração da entropia se dá por:

Δ s = c p ln ⁡ T 2 T 1 - R ln ⁡ P 2 P 1           →     Δ s = 485 J K g K

Resposta

  1. Entrada da tubina:   T 01 = 1572   K ;   P 01 = 698   k P a
  2. Saída da turbina: T 02 = 1041   K       ; P 02 = 30   k P a

Variação isentrópica:

→     Δ s = 485 J K g K

Diagrama Ts:

Ver Outros Exercícios desse livro