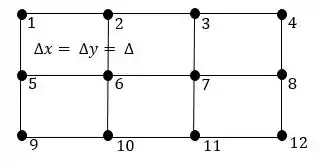
Qual é a equação de condução de calor transiente de diferenças avançadas correta para o nó 6 do sólido retangular mostrado na Fig. P5-140 se sua temperatura no momento anterior ( ∆ t ) for T 6 * ? a T 6 i + 1 =k ∆ t ρ C p ∆ ² T 5 * +T 2 * +T 7 * +T 10 * +1 - 4 k ∆ t ρ C p ∆ ² T 6 * ² ² ( b ) T 6 i + 1 =k ∆ t ρ C p ∆ ² T 5 * +T 2 * +T 7 * +T 10 * +1 - k ∆ t ρ C p ∆ ² T 6 * ² ² ( c ) T 6 i + 1 =k ∆ t ρ C p ∆ ² T 5 * +T 2 * +T 7 * +T 10 * +2 k ∆ t ρ C p ∆ ² T 6 * ² ² ( d ) T 6 i + 1 =2 k ∆ t ρ C p ∆ ² T 5 * +T 2 * +T 7 * +T 10 * +1 - 2 k ∆ t ρ C p ∆ ² T 6 * ² ² ( e ) T 6 i + 1 =2 k ∆ t ρ C p ∆ ² T 5 * +T 2 * +T 7 * +T 10 * +1 - 4 k ∆ t ρ C p ∆ ² T 6 * ² ²

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 140

Qual é a equação de condução de calor transiente de diferenças avançadas correta para o nó do sólido retangular mostrado na Fig. P5-140 se sua temperatura no momento anterior for ?

Passo 1

Pois considera-se a Lei de Fourier de cada direção até o nó em questão, para aplicar-se o método de diferenças finitas, contabilizando tal nó vezes e cada um dos pontos da vizinhança apenas vez, esses valores foram agrupados após a temperatura ser evidenciada e passaram a multiplicas a condutividade térmica .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro