Em uma fábrica, placas de bronze molhadas de 50 cm x 50 cm que saem de um banho de água devem ser secas passando através de uma seção onde ar a 1 atm e 25°C é soprado em paralelo às suas superfícies a 6 m/s. Considerando que as placas estão a 15°C e não existem pontos secos, determine a taxa de evaporação de ambos os lados da placa.
Passo 1
Nossa situação é a seguinte:
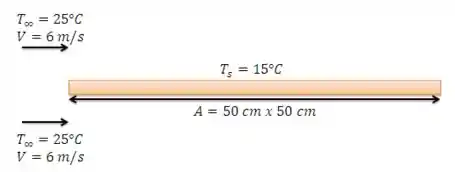
Temos ar a 1 atm e 25°C escoando sobre os dois lados de placas de cobre com velocidade . As placas são quadradas com lado . A temperatura das placas é .
Sabendo disso devemos calcular a taxa de evaporação pelos dois lados da placa. Vamos começar calculando o coeficiente de transferência de massa para o sistema; e, então, a partir do coeficiente teremos condições de calcular a taxa de evaporação de água pela superfície da placa. Vamos lá???
Passo 2
Nosso primeiro passo é determinar o coeficiente de transferência de massa. Para isso vamos começar calculando o número de Reynolds. Ele é dado por:
Para o ar com e :
Então:
Nosso próximo passo é calcular o número de Schmidt. Ele pode ser determinado por:
A difusividade do vapor de água no ar a 25°C (298 K) e 1 atm é . Então, o número de Schmidt é:
O próximo passo é utilizar a correlação de Sherwood. Para escoamento em placa plana, nós temos:
O último passo é utilizar o número de Sherwood para determinar o coeficiente de transferência de massa:
Passo 3
Vamos considerar que o ar não se difunde na água líquida. Então, trata-se de um processo de difusão de A em B estagnado. A taxa de difusão de A em B estagnado é dado por:
Antes de determinar a taxa precisamos determinar a concentração e as frações molares de água na superfície e no ar. Para uma mistura gasosa a concentração é:
O enunciado nos deu o valor de pressão e de temperatura, mas precisamos converter nossas unidades.
E agora sim, colocar isso na nossa equação da concentração:
Na superfície do filme o ar está saturado de água. Então . No ar vamos considerar que a quantidade de água é muito pequena, então . A pressão de vapor da água a 15°C é .
A fração molar é dada por:
Portanto
Substituindo a concentração e as frações molares na equação de taxa:
Para transformar em taxa mássica que evapora devemos multiplicar pela massa molar da água. Assim:
Resposta
A taxa de evaporação é .