Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 8
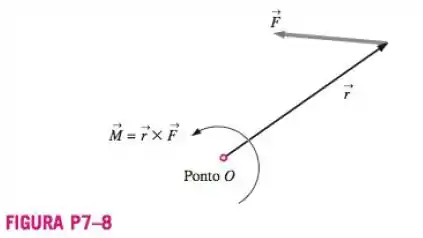
O é formado pelo produto vetorial de um braço de momento e por uma força aplicada , conforme representação na Figura P7-8. Quais são as dimensões primárias do torque? Liste suas unidades em unidades primárias e em unidades inglesas primárias.
Passo 1
Temos o sistema primário, que representamos da seguinte forma:
Para unidade de espaço, comprimento ou largura:
Para unidade de tempo:
Temperatura:
Intensidade de corrente elétrica:
Quantidade de matéria:
Intensidade luminosa:
Este é o sistema primário.
Nosso objetivo é escrever o torque neste sistema.
Passo 2
Temos a formula do torque, vamos determinar o que é a força:
Pela segunda lei de Newton, temos:
E temos que é comprimento do nosso braço, aonde a força é aplicada.
Portanto, para o torque temos:
Passo 3
Agora que determinamos o torque no sistema primário de unidades, vamos colocar no :
Para :
Sabendo das unidades do , vamos substituir a fórmula do torque:
Passo 4
Agora vamos colocar a unidade do torque no sistema de unidades inglesa:
Para o sistema inglês:
Substituindo na fórmula:
Resposta
Sistema primário:
Sistema internacional:
Sistema inglês: