A formulação de diferenças finitas da condução de calor permanente bidimensional em um meio com geração de calor e condutividade térmica constante é dada por: T m - 1 , n - 2 T m , n + T m + 1 , n ∆ x 2 + T m , n - 1 - 2 T m , n + T m , n + 1 ∆ y 2 + e ˙ m , n k = 0 em coordenadas retangulares. Modifique essa relação para o caso tridimensional.

Modificando a equação, ela fica assim... T m - 1 , n , o - 2 T m , n , o + T m + 1 , n , o ∆ x 2 + T m , n - 1 , o - 2 T m , n , o + T m , n + 1 , o ∆ y 2 + T m , n , o - 1 - 2 T m , n , o + T m , n , o + 1 ∆ z 2 + e ˙ m , n , o k = 0 Lembrando que em outros lugares a letra para o ponto nodal para direção z pode ser diferente da que adotamos aqui...

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 7

A formulação de diferenças finitas da condução de calor permanente bidimensional em um meio com geração de calor e condutividade térmica constante é dada por:

em coordenadas retangulares. Modifique essa relação para o caso tridimensional.

Passo 1

Bom, vamos lá...

Sabemos que a codução de calor permante bidimensional em coordenadas retangulares e dada pela equação do enunciado. Note que essa equação equivale a direções no plano como por exemplo direção e , as letras e referem-se as direções nodais.

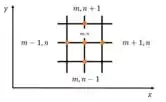
Muito bem! Agora que lembramos esse conceito, basta acrescentarmos a coordenada tridimensional, ou seja, na direção e vamos usar a letra para referenciar o ponto nodal nessa direção ok?

Resposta

Modificando a equação, ela fica assim...

Lembrando que em outros lugares a letra para o ponto nodal para direção pode ser diferente da que adotamos aqui...

Ver Outros Exercícios desse livro