Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 23

Considere uma grande placa de urânio de 5   c m de espessura e condutividade térmica k = 34 w m ∙ K em que o calor é gerado uniformemente a uma taxa constante de e ˙ = 6 × 10 5 W m 3 . Um dos lados da placa é isolado, enquanto o outro lado é submetido à convecção para o ambiente a 30 ° C , com coeficiente de transferência de calor h = 60 W m 2 ∙ K . Considerando 6 nós igualmente espaçados com espaçamento nodal de 1   c m , a obtenha a formulação de diferenças finitas desse problema e ( b ) determine as temperaturas nodais sob condições permanentes, resolvendo essas equações.

Passo 1

Vamos lá, como primeiro passo nós temos que extrair os dados do enunciado:

L = 5   c m ; T ∞ = 30 ° C ;   k = 34 W m ∙ k ; h =   60 W m 2 ∙ k   ;   ∆ x = 1   c m ;   m = 6 ;   e ˙ = 6 × 10 5 W m 3

Beleza! O exercício quer que nos separemos em 6 nós, logo ficará assim...

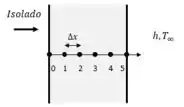
O nosso nó 0 se encontra isolado, logo aplicando o conceito de espelho gerando uma reflexão, podemos usar a seguinte equação geral para os nós 1, 2, 3 e 4 que são nós interiores:

T m - 1 - 2 T m + T m + 1 ∆ x 2 + e ˙ k = 0

Passo 2

Usando nossa equação geral, basta aplicarmos nos pontos agora.

Nó 0:

T 1 - 2 T 0 + T 1 ∆ x 2 + e ˙ k = 0

Nó 1:

T 0 - 2 T 1 + T 2 ∆ x 2 + e ˙ k = 0

Nó 2:

T 1 - 2 T 2 + T 3 ∆ x 2 + e ˙ k = 0

Nó 3:

T 2 - 2 T 3 + T 4 ∆ x 2 + e ˙ k = 0

Nó 4:

T 3 - 2 T 4 + T 5 ∆ x 2 + e ˙ k = 0

Para o nó 5 que se encontra na extremidade a formulação se dará pelo balanço de energia que ficará assim:

h T ∞ - T 5 + k T 4 - T 5 ∆ x + e ˙ ∆ x 2 = 0

Resposta

Usando um programa que resolve varias equações simultaneamente, encontraremos as seguintes temperaturas:

T 0 = 552,1 ° C

T 1 = 551,2 ° C

T 2 = 548,5 ° C

T 3 = 544,1 ° C

T 4 = 537,9 ° C

T 5 = 530,0 ° C

Ver Outros Exercícios desse livro