Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 14.Problemas - Ex. 38

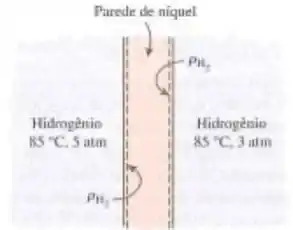
Gás hidrogênio a 85°C é mantido a pressões constantes de 5 atm e 3 atm nos lados oposto de uma parede de níquel de 0,1 mm de espessura. Determine a taxa de difusão molar por unidade de área através da parede.

Passo 1

Booora continuar galerinhaaa!!!

Então, nesta questão nós queremos achar qual a difusão em massa do gás hidrogênio, não é?

E para isso nós usamos a taxa de difusividade dele, ok?

Bora ver a fórmula?

m d i f u s ã o ˙ = A D A B × ρ H 2 , 1 - ρ H 2 , 2 L

E o que nós sabemos?

A = 1   m ²

L = 0,1   m m = 0,00 01   m

O coeficiente de difusão binária é tabelado, e para o hidrogênio atravessando uma parede de níquel:

D A B = 1,2 × 10 - 12 m 2 s

A única coisa que precisamos é da densidade mássica, certo?

Bora lá !

Passo 2

Se lembram como calcular a densidade mássica?

ρ H 2 = C H 2 × M H 2

Lembrando que:

M H 2 = 2,016 k g k m o l

Só precisamos da densidade molar!

Vamos ver como calcular?

C H 2 , 1 = ξ × P H 2 , 1

C H 2 , 2 = ξ × P H 2 , 2

Onde ξ é a solubilidade.

Nós sabemos que:

P H 2 , 1 = 5   a t m × 1 , 01325   b a r 1   a t m = 5,066   b a r

P H 2 , 2 = 3   a t m × 1,01325   b a r 1   a t m = 3,039   b a r

E quanto a solubilidade?

Simples !! Vamos olhar a tabela abaixo:

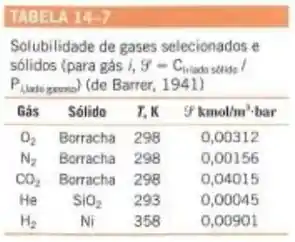
Então:

ξ = 0,00901 k m o l m ³ . b a r

Olha que tooop!!

Agora é só colocar tudo isso na fórmula:

C H 2 , 1 = 0,00901 k m o l m ³ . b a r × 5,066   b a r = 0,04565 k m o l m 3

C H 2 , 2 = 0,00901 k m o l m ³ . b a r × 3,039   b a r = 0,02739 k m o l m 3

Isso aeeee!!

Agora só precisamos colocar na densidade mássica:

ρ H 2 , 1 = 0,04565 k m o l m 3 × 2,016 k g k m o l = 0,0 92   k g m ³

ρ H 2 , 2 = 0,02739 k m o l m 3 × 2,016 k g k m o l = 0,0 55   k g m ³

Passo 3

Agora que temos tudo que precisamos bora colocar na difusividade:

m d i f u s ã o ˙ = 1   m ² 1,2 × 10 - 12 m 2 s × 0,092   k g m ³ - 0,055   k g m ³ 0,00 01   m

m d i f u s ã o ˙ = 4,44 × 10 - 10 k g s

Então a taxa de difusão do hidrogênio através da parede de níquel será de 4,44 × 10 - 1 0 k g s .

E finalizamos mais umaa !!

Resposta

4,44 × 10 - 10 k g s

Ver Outros Exercícios desse livro