Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 14.Problemas - Ex. 31
Considere um copo de água em uma sala à temperatura de 15°C e 97 kPa. Considerando que a umidade relativa do ar na sala é 100% e água e ar estão em fase de equilíbrio térmico, determine (a) a fração molar do vapor de água no ar e (b) a fração molar do ar na água.
Passo 1
Vamo que vamo galeeera !!
Preparados para mais uma?!
Bom, na letra (a) nós queremos achar a fração molar do vapor de água no ar, certo?
Se nós considerarmos que o ar e o vapor de água são gases ideais nós poderemos calcular a fração molar como:
Olhando a Tabela A-9, quando a temperatura é 15°C:
Então galerinha nós já temos tudo que precisamos:
Agora é só nós substituirmos:
A letra (a) foi tranquila, bora seguir pra (b) !!
Passo 2
Na letra (a) nós achamos a pressão do vapor de água e na letra (b) nós queremos a pressão do ar, certo?
E como?
Para achar a fração molar do ar na água nós usamos a Lei de Henry, se lembram?
Se não lembram não tem problema, eu mostro pra vocês:
Bom, nossa pressão total é de 97 kPa apenas 1,7051 kPa é devido ao vapor de água, então o que sobra é a pressão causada pelo ar, ok?
Substituindo:
E quanto a constante de Henry? Vamos olhar a tabela:
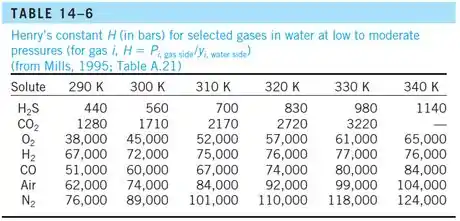
Já vimos que precisamos da temperatura em kelvin, então:
Como não temos nada antes de 290K vamos usar a constante para 290K, tudo bem?
E agora que temos tudo só precisamos substituir:
E finalizamos mais uma !!