Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 103

Um incômodo comum em carros nos meses de inverno é a formação de névoa sobre as superfícies do vidro, que bloqueia a visão. A forma prática de resolver esse problema é soprar ar quente ou colocar resistências elétricas aquecedoras nas superfícies internas. Considere o vidro traseiro do carro que consiste de vidro de 0,4   c m de espessura ( k = 0,84 W m ∙ K e α = 0,39 × 10 - 6 m 2 s . Fios aquecedores de espessura desprezível são fixados na face interna do vidro, com 4   c m de intervalo. Cada fio gera calor a uma taxa de 10 W m de comprimento. Inicialmente, o carro todo, incluindo as janelas, está na temperatura externa T o = - 3 ° C . Os coeficientes de transferência de calor nas superfícies interna e externa do vidro podem ser considerados   h i = 6 e h o = 20 W m 2 ∙ K , respectivamente. Usando o método explícito de diferenças finitas com tamanho da malha de ∆ x = 0,2   c m   ao longo da espessura e ∆ y = 1   c m   no sentido normal aos fios aquecedores, determine a distribuição de temperatura ao longo de todo o vidro 15 minutos após os aquecedores serem ligados. Além disso, determine a distribuição de temperatura quando são atingidas as condições permanentes.

Passo 1

Muito bem, anotando os dados do enunciado, teremos que:

k = 0,84 W m ∙ K ;   α = 0,39 × 10 - 6 m 2 s ; T i = T o = - 3 ° C ; h i = 6 W m 2 ∙ K  

h o = 20 W m 2 ∙ K ;   ∆ x = 0,2   c m   ;   ∆ y = 1   c m  

Analisando os nós do nosso problema, podemos ver que há uma simetria...

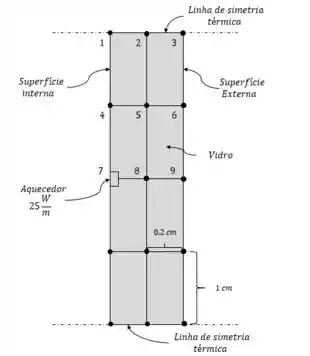
O balanço de energia para o método explícito pode ser expresso como:

∑ T o d o s   o s   l a d o s Q ˙ i + E ˙ e l e m e n t o i = ρ V e l e m e n t o c p T m i + 1 - T m i ∆ t

Passo 2

Agora podemos aplicar o balanço de energia nos 9 nós, devido a simetria...

N ó   1 :

h i ∆ y 2 T i - T 1 i + k ∆ x 2 T 4 i - T 1 i ∆ y + k ∆ y 2 T 2 i - T 1 i ∆ x = ρ c p ∆ x 2 ∆ y 2 T 1 i + 1 - T 1 i ∆ t

N ó   2 :

k ∆ y 2 T 1 i - T 2 i ∆ x + k ∆ y 2 T 3 i - T 2 i ∆ x + k ∆ x T 5 i - T 2 i ∆ y = ρ c p ∆ x ∆ y 2 T 2 i + 1 - T 2 i ∆ t

N ó   3 :

h o ∆ y 2 T o - T 3 i + k ∆ x 2 T 6 i - T 3 i ∆ y + k ∆ y 2 T 2 i - T 3 i ∆ x = ρ c p ∆ x 2 ∆ y 2 T 3 i + 1 - T 3 i ∆ t

N ó   4 :

h i ∆ y T i - T 4 i + k ∆ x 2 T 1 i - T 4 i ∆ y + k ∆ x 2 T 7 i - T 4 i ∆ x + k ∆ y T 5 i - T 4 i ∆ x = ρ c p ∆ y ∆ x 2 T 4 i + 1 - T 4 i ∆ t

N ó   5 :

k ∆ y T 4 i - T 5 i ∆ x + k ∆ y T 6 i - T 25 i ∆ x + k ∆ x T 8 i - T 5 i ∆ y + k ∆ x T 2 i - T 5 i ∆ y = ρ c p ∆ x ∆ y T 5 i + 1 - T 5 i ∆ t

N ó   6 :

h o ∆ y T i - T 6 i + k ∆ x 2 T 3 i - T 6 i ∆ y + k ∆ x 2 T 9 i - T 6 i ∆ y + k ∆ y T 5 i - T 6 i ∆ x = ρ c p ∆ y ∆ x 2 T 6 i + 1 - T 6 i ∆ t

N ó   7 :

12 ,   5   W   h i ∆ y 2 T i - T 7 i + k ∆ x 2 T 4 i - T 7 i ∆ y + k ∆ y 2 T 8 i - T 7 i ∆ x = ρ c p ∆ y 2   ∆ x 2 T 7 i + 1 - T 7 i ∆ t

N ó   8 :

k ∆ y 2 T 7 i - T 8 i ∆ x + k ∆ y 2 T 9 i - T 8 i ∆ x + k ∆ x T 5 i - T 8 i ∆ y = ρ c p ∆ y 2 ∆ x T 8 i + 1 - T 8 i ∆ t

N ó   9 :

h o ∆ y 2 T o - T 9 i + k ∆ x 2 T 6 i - T 9 i ∆ y + k ∆ y 2 T 8 i - T 9 i ∆ x = ρ c p ∆ y 2 ∆ x 2 T 9 i + 1 - T 9 i ∆ t

Passo 3

No método explícito é necessário aplicar um critério de estabilidade, e para expressarmos esse critério, utilizaremos o coeficiente T 6 i em T 6 i + 1 , pois é o nó que mais será exposto a convecção por unidade de volume.

Rearranjando a equação para o nó 6 temos...

T 6 i + 1 = 1 - 2 α ∆ t h o k ∆ x + 1 ∆ y 2 + 1 ∆ x 2 T 6 i + 2 α t h o k ∆ x T 0 + T 3 i + T 9 i ∆ y 2 + T 5 i ∆ x

Portanto, o critério de estabilidade pode ser expresso como:

1 - 2 α ∆ t h o k ∆ x + 1 ∆ y 2 + 1 ∆ x 2 ≥ 0

∆ t ≤ 1 2 α ∆ t h o k ∆ x + 1 ∆ y 2 + 1 ∆ x 2

Determinando o passo de tempo:

∆ t ≤ 1 2 × 0,39 × 10 6 m 2 s 20 W m 2 ∙ K 0,84 W m ∙ K 0,002   m + 1 0,002   m 2 + 1 0,01   m 2 = 4,7   s  

Logo devemos escolher um passo de tempo menor do que o encontrado, ou seja, vamos escolher um passo de tempo de ∆ t = 4   s .

Resposta

Por fim a distribuição de temperatura ao longo do vidro após 15 min será de:

T 1 = - 0,73 ° C

T 2 = - 0,84 ° C

T 3 = - 0,98 ° C

T 4 = 0,68 ° C

T 5 = - 0,03 ° C

T 6 = - 2,0 ° C

T 7 = 36,0 ° C

T 8 = 32,0 ° C

T 9 = 29,2 ° C

Em regime permanente:

T 1 = - 0 , 69 ° C

T 2 = - 0 , 79 ° C

T 3 = - 0,9 3 ° C

T 4 = 0 , 71 ° C

T 5 = - 0,0 05 ° C

T 6 = - 2,0 ° C

T 7 = 36 , 1 ° C

T 8 = 32,0 ° C

T 9 = 29,2 ° C

Ver Outros Exercícios desse livro