Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 1.Problemas - Ex. 16

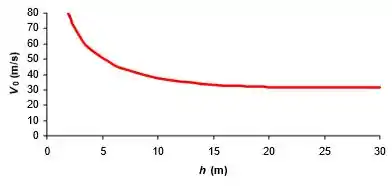
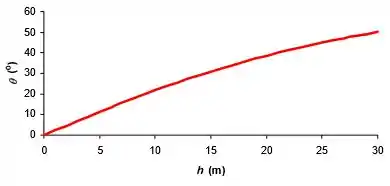
Os ingleses aperfeiçoaram o arco e flecha como arma após o período Medieval. Nas mãos de um arqueiro hábil, a arma era considerada precisa a distâncias de 100 metros ou mais. Considerando que a altitude máxima de uma flecha seja h = 10 m no trajeto para um alvo a 100 m de distância do arqueiro, e desprezando a resistência do ar, estime a velocidade e o ângulo com os quais a flecha deve deixar o arco. Trace os gráficos da velocidade e do ângulo de disparo como funções da altura h.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Considerando que a flecha tem velocidade e faz um ângulo com a horizontal. Sabemos que:

Pela segunda lei de Newton, sabemos que:

Logo:

Também temos que:

Portanto:

Integrando os dois lados e aplicando os limites:

Logo:

Já para o eixo horizontal, temos que:

Logo:

Portanto:

Passo 2

Agora, vamos apenas trabalhar com as equações encontradas no passo 1. Assim, teremos:

Logo:

Substituindo para acharmos

Da equação 3, temos

Logo:

Com as expressões abaixo, basta plotar os gráficos:

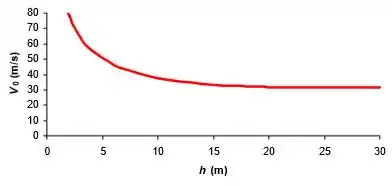
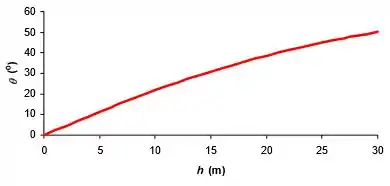
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o sistema de três equações com três incógnitas usando o EES: 2 x - y + z = 5 3 x 2 + 2 y = z + 2 x y + 2 z = 8

A força de reação movida por um motor a jato para impulsionar um aeroplano para frente é chamada de empuxo e o empuxo desenvolvido por um motor de um Boening 777 é de cerca de 85.000I b f . Expresse e

Resolva o sistema de três equações com três incógnitas usando o EES: x 2 y - z = 1 x - 3 y 0,5 + x y = - 2 x + y - z = 2

Determine uma raiz real positiva dessa equação usando o EES: 2 x 3 - 10 x 0,5 - 3 x = - 3

Resolva o sistema de duas equações com duas incógnitas usando o EES: x 3 - y 2 = 7,75 3 x y + y = 3,5