Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 14.Problemas - Ex. 92

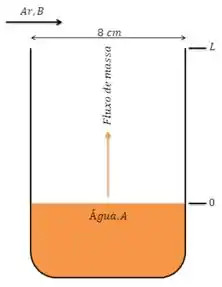
Uma jarra de 8 cm de diâmetro interno e 30 cm de altura, com água até a metade, é deixada em uma sala seca a 10°C e 0,92 atm com superfície superior aberta. Se água também é mantida a 10°C o tempo todo, determine o tempo necessário para a água evaporar completamente.

Passo 1

Vamos reunir nossas informações. Temos água (composto A) evaporando no ar (composto B) nas condições de P = 0,92   a t m = 93.219   P a e T = 10 ° C = 2 83   K . As propriedades da água são:

ρ A = 999,7   k g / m 3

M A = 18   k g / k m o l

O processo de transferência de massa ocorre dos pontos z=0 até z= 15   c m = L . Sabemos que no topo (z= L ) não há água. Então y A , L = 0 .

Vamos considerar que na interface líquido-gás (z=0), o ar está saturado de vapor de água. Então P A , 0 = P v a p o r = 1,2276   k P a . Sabemos que a jarra tem diâmetro de D = 8   c m e que a água ocupa metade do volume total, ou seja, está em uma altura de 15 cm no início do processo. Devemos determinar o tempo necessário para evaporar toda a água. Vamos lá?

Passo 2

Nosso primeiro passo será determinar o fluxo molar de evaporação da água. Vamos considerar que o ar não se difunde para o interior da água líquida. Então nosso processo é uma difusão de A em B estagnado. O fluxo nesta condição é dado por:

N A = D A B C L ln ⁡ 1 - y A , L 1 - y A , 0

Precisamos então da difusividade da água nestas condições, além da concentração molar e da fração molar y A , 0 . De acordo com a tabela 14-2 do livro:

D A B = 2,5 x 10 - 5   m 2 / s

Para T = 298   K e P = 1   a t m = 101,325   k P a . Para obter a difusividade nas condições do problema vamos usar a relação:

D A B 1 D A B 2 = P 2 P 1 T 1 T 2 3 2

D A B 2 = D A B 1 P 1 P 2   T 2 T 1 3 2

D A B 2 = 2,5 x 10 - 5 x 101,3 25 93,219 x   283 298 3 2

D A B 2 = 2,5 x 10 - 5   m 2 / s

Vamos agora para a concentração molar. Para difusão em gases ela é dada por:

C = P R T

C = 93.219 8.314 x 283

C = 0,0396   k m o l / m 3

A última parte antes de calcularmos o fluxo é determinar y A , 0 :

y A , 0 = P A , 0 P

y A , 0 = 1,2276 93,219

y A , 0 = 0,0132

Voltando para a equação de fluxo, vamos utilizar um L médio de 22,5 cm, já que a distância da interface de água até o topo da jarra varia de 15 cm até 30 cm. Portanto

N A = 2,5 x 10 - 5 x 0,0396 0,225 ln ⁡ 1 - 0 1 - 0,0132

N A = 5,87 x 10 - 8   k m o l / m 2 s

Passo 3

Vamos agora utilizar este fluxo para estimar o tempo necessário para evaporar toda a água da jarra. O fluxo também pode ser descrito como:

N A = m o l s A x t

Precisamos então do número de mols de água no início e a área da jarra.

Vamos primeiro determinar a área da jarra. Ela é dada por:

A = π x D 2 4

A = π x 0,08 2 4

A = 0,005   m 2

Vamos agora calcular o volume de água que evaporou. Sabemos que inicialmente havia água em uma altura de 15 cm. Então

V = A x h

V = 0,005 x 0,15

V = 7,54 x 10 - 4   m 3

Vamos agora usar a densidade e a massa molar para converter este volume em mols de água:

ρ = m V

M = m n

m = ρ V = M n

n = ρ V M

n = 999,7 x 7,54 x 10 - 4 18

n = 4,19 x 10 - 2   k m o l

Voltando para equação de fluxo:

N A = n A x t

t = n A x N A

t = 4,19 x 10 - 2 0,005 x 5,87 x 10 - 8

t = 1,42 x 10 8   s = 4,5   a n o s

Resposta

Nestas condições o tempo para evaporar toda a água é de t = 4,5   a n o s .

Ver Outros Exercícios desse livro