Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 14.Problemas - Ex. 94

Metanol ( ρ = 791 kg/m3 e M = 32 kg/kmol) é evaporado em um tubo de Stefan com área transversal uniforme de 0,8 cm2. Inicialmente, a superfície de metanol foi de 10 cm do topo do tubo e, depois de um tempo, a superfície de metanol chegou a 26 cm do topo do tubo. A pressão de vapor do metanol é 17 kPa, e a concentração de metanol no topo do tubo é zero. Considerando que todo o processo foi realizado a 25°C e 1 atm, determine a taxa de evaporação de metanol em kg/h. A difusividade da massa de metanol no ar é D A B = 0,162 cm2/s.

Passo 1

Vamos reunir nossas informações. Temos metanol evaporando em um tubo de Stefan nas condições de P = 1   a t m = 101.325   P a e T = 2 5 ° C = 29 8   K . As propriedades do metanol são:

ρ A = 791   k g / m 3

M A = 32   k g / k m o l

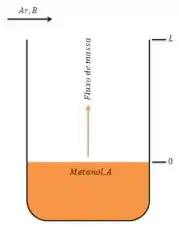
O processo de transferência de massa ocorre dos pontos z=0 até z= L . Sabemos que no topo (z= L ) não há metanol. Então y A , L = 0 .

Vamos considerar que na interface líquido-gás (z=0), o ar está saturado de metanol. Então P A , 0 = P v a p o r = 17   k P a . Sabemos que o tubo tem área de A = 0,8   c m 2 e que a variação de altura do metanol foi de 16 cm. Além disso, temos que a difusividade do metanol em ar é de D A B = 1,62 x 10 - 5   m 2 / s . O exercício nos pede para determinar a taxa de evaporação do metanol em kg/h. Vamos lá?

Passo 2

Vamos começar fazendo algumas considerações. Primeiro, vamos assumir que o ar não se difunde no metanol ( N B = 0 → difusão de A em B estagnado). Como L varia ao longo do processo vamos usar uma média de 10 cm e 26 cm, ou seja, usaremos L = 18   c m . O fluxo molar de metanol pode ser calculado por:

N A = D A B C L ln ⁡ 1 - y A , 0 1 - y A , L

Então para calcular o fluxo só nos falta determinar a concentração molar ( C ) e a fração molar de metanol na interface ( y A , 0 ). A concentração molar para difusão em um gás é dada por:

C = P R T

C = 101.300 8.314 x 298

C = 0,0409   k m o l / m 3

A fração molar pode ser calculada por:

y A , 0 = P A , 0 P

y A , 0 = 17 101,3

y A , 0 = 0,168

O fluxo de metanol é:

N A = 1,62 x 10 - 5 x 0,0409 0,18 ln ⁡ 1 - 0 1 - 0,168  

N A = 1,22 x 10 - 7   k m o l / m 2 s

Passo 3

O exercício nos pede taxa mássica. Então nosso próximo passo será transformar o fluxo molar em taxa molar. Para isso usaremos a relação:

N ˙ A = A x N A

N ˙ A = 0,8 x 10 - 4 x 1,22 x 10 - 7

N ˙ A = 9,73 x 10 - 12   k m o l / s

Agora que já temos a taxa molar vamos multiplicar este valor pela massa molar do metanol para obter a taxa mássica. Assim:

m ˙ A = M A x N ˙ A

m ˙ A = 32 x 9,73 x 10 - 12

m ˙ A = 3,11 x 10 - 10   k g / s

m ˙ A = 1,12 x 10 - 6   k g / h

Resposta

A taxa de evaporação do metanol é de m ˙ A = 1,12 x 10 - 6   k g / h .

Ver Outros Exercícios desse livro