Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 211

A massa total do tipo de helicóptero mostrado é de 1000   k g . A pressão do ar é a atmosférica na saída. Considere que o escoamento seja permanente e unidimensional. Trate o ar como incompressível nas condições-padrão e calcule, para uma posição em que o aparelho paira no ar, a velocidade do ar saindo da aeronave e a potência mínima que deve ser fornecida ao ar pela hélice.

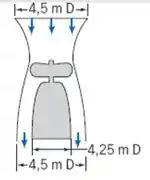
Passo 1

A equação da Primeira Lei da Termodinâmica se dá:

Q ˙ - W s ˙ - W ˙ c i s a l h - W ˙ o u t r o s = ∂ ∂ t ∫ V C e ρ d ∀ + ∫ S C u + p v + V 2 2 + g z ρ V d A

Considerações Iniciais:

  1. Escoamento Uniforme;
  2. Escoamento Estacionário;
  3. Fluído Incompressível;
  4. Sem Variação de Altura e de Energia Interna ( ∆ z = ∆ u = 0 ) ;
  5. Sem Troca de Calor ( Q = 0 ) ;
  6. Somente W s ;
  7. Pressões iguais.

Passo 2

Pelas considerações feitas no passo 1, temos:

- W s ˙ = ∫ S C V 2 2 ρ V d A

- W s ˙ = V 1 2 2 ⋅ - ρ V 1 A 1 V 2 2 2 ⋅ ρ V 2 A 2

Assim, pela continuidade m ˙ 1 = m ˙ 2 = m ˙

- W s ˙ = m ˙ V 2 2 2 - V 1 2 2

Passo 3

Determinando a velocidade do ar saindo da aeronave.

Calculando as áreas:

A 1 = π ⋅ D 1 2 4 = π ⋅ 4,5 2 4 = 15,9   m 2

A 2 = π ⋅ ( D 1 2 - D 2 2 ) 4 = π ⋅ ( 4,5 2 - 4,25 2 ) 4 = 1,7   m 2

Aplicando a equação da quantidade de movimento, temos:

F = F S + F B - ∫ V C a r ρ d ∀ = ∂ ∂ t ∫ V C V ρ   d ∀ + ∫ S C V ( ρ V ) d A = 0

p 1 A 1 - m g = v 1 - ρ V 1 A 1 + v 2 ρ V 2 A 2

Sendo:

v 1 = - V 2 ;

v 2 = - V 2 ;

p a t m = p 1 + 1 2 ρ V 1 2 → p a t m = 0 → p 1 = - 1 2 ρ V 1 2 .

Temos:

- 1 2 ρ V 1 2 A 1 - m g = ρ V 1 A 1 V 2 - ρ V 2 A 2 V 2

Pela continuidade:

V 1 A 1 = V 2 A 2 → V 1 = V 2 A 2 A 1

Então:

- 1 2 ρ V 1 2 A 1 - m g = - ρ V 2 A 2 ( V 2 - V 1 )

- 1 2 ρ V 1 2 A 1 = - 1 2 ρ V 1 V 2 A 2 = - 1 2 ρ V 2 A 2 A 1 A 2 V 2 = - 1 2 ρ V 2 2 A 2 2 A 1

- 1 2 ρ V 2 2 A 2 2 A 1 - m g = - ρ V 2 2 A 2 1 - V 1 V 2 2

- 1 2 ρ V 2 2 A 2 2 A 1 - m g = - ρ V 2 2 A 2 1 - A 2 A 1

Isolando V 2 :

m g = V 2 2 ρ A 2 1 - 1 2 A 2 A 1

V 2 = m g ρ A 2 1 - 1 2 A 2 A 1

Sendo:

m = 1000   k g ;

g = 9,8   m / s 2 ;

ρ = 1 , 222   k g / m 3 ;

Temos:

V 2 = 1000 ⋅ 9,8 1,222 ⋅ 1,7 ⋅ 1 - 1 2 1,7 15,9 = 70,6   m / s

Passo 4

Determinando a potência mínima que deve ser fornecida ao ar pela hélice.

Voltando na equação do Passo 2:

- W s ˙ = m ˙ V 2 2 2 - V 1 2 2

- W s ˙ = m ˙ 2 V 2 2 - V 1 2 = m ˙ V 2 2 2 1 - V 1 2 V 2 2 = m ˙ V 2 2 2 1 - A 2 A 1 2

Sendo m ˙ = ρ V 2 A 2 :

- W s ˙ = ρ V 2 3 A 2 2 1 - A 2 A 1 2

Temos:

- W s ˙ = ρ V 2 3 A 2 2 1 - A 2 A 1 2

- W s ˙ = 1,222 ⋅ 70,6 3 ⋅ 1,7 2 1 - 1,7 15,9 2 =

W s = - 361   k W

Resposta

V 2 = 70,6   m / s

W s = - 361   k W

Ver Outros Exercícios desse livro