Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 174
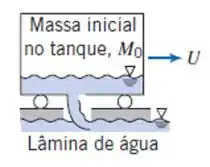
O tanque móvel mostrado deve ser desacelerado pelo abaixamento de uma concha que capta água de um reservatório. A massa e a velocidade iniciais do tanque, com seu conteúdo, são e , respectivamente. Despreze forças externas de pressão e de atrito e considere que a pista seja horizontal. Aplique as equações da continuidade e da quantidade de movimento para mostrar que, em qualquer instante, . Obtenha uma expressão geral para com uma função do tempo.
Passo 1
Considerações Iniciais:
- Escoamento em estado estacionário;
- Escoamento incompressível;
- Escoamento com velocidade constante ;
- Escoamento uniforme;
- Força de corpo desprezível;
- Força de resistência desprezível.
Passo 2
Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:
Como estamos analisando um sistema , temos:
Não há resistência ne força de campo, então, :
Não temos a variação das propriedades com o tempo, então:
Assim:
Então:
Sendo:
.
Temos:
Passo 3
Aplicando as equações da continuidade e da quantidade de movimento para mostrar que, em qualquer instante, .
Temos que e , assim:
Passo 4
Obtendo uma expressão geral para com uma função do tempo.
Sendo :
Integrando:
Rearranjando: