Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 14.Problemas - Ex. 142
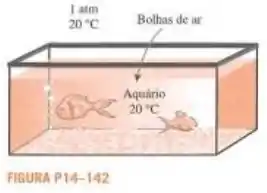
A necessidade de oxigênio dos peixes nos aquários geralmente é suprida forçando ar para o fundo do aquário com um compressor. As bolhas de ar proporcionam uma grande área de contato entre a água e o ar, e, quando as bolhas sobem, os gases oxigênio e nitrogênio do ar se dissolvem na água enquanto um pouco de água evapora para dentro das bolhas. Considere um aquário mantido a uma temperatura ambiente de o tempo todo. As bolhas de ar sobem para a superfície livre de água em . Supondo que o ar que entra no aquário esta completamente seco e o diâmetro das bolhas de ar é de , determine a fração molar do vapor de água no centro da bolha quando sai do aquário. Considere que não há nenhum movimento de fluido na bolha, de modo que o vapor de água se propaga na bolha apenas por difusão.
Passo 1
Dados fornecidos:
Temperatura ambiente:
Tempo em que o ar sobe para a superfície livre:
Diâmetro das bolhas de ar:
Raio das bolhas de ar:
Propriedades:
Pela Tabela 14-6
Constante de Henry para o oxigênio dissolvido na água a :
Pela Tabela A-9
Pressão de saturação da água a :
Pressão ambiente:
Premissas:
1) As bolhas de ar estão inicialmente completamente secas.
2) As bolhas são esféricas e possuem simetria sobre o ponto médio.
3) O ar é fracamente solúvel em água e, portanto, a lei de Henry é aplicável.
4) Os efeitos de convecção na bolha são desprezíveis.
5) A pressão e a temperatura das bolhas de ar permanecem constantes a e .
6) Tanto o ar quanto o vapor são gases ideais.
Passo 2
Podemos começar calculando a difusividade de massa do vapor de água no ar a usando a Equação 14-15. Assim temos:
Substituindo os temos da equação pelos dados obtidos, temos:
Passo 3
Temos que este problema é análogo ao problema de condução de calor transiente unidimensional em uma esfera com temperatura superficial especificada e, portanto, pode ser resolvido da mesma forma.
Agora, vamos calcular o número de Fourier da transferência de massa para usando a seguinte expressão:
Substituindo os temos da equação pelos dados obtidos, temos:
Passo 4
Observando que o ar na bolha na interface ar-água será saturado, assim, a pressão de vapor na interface pode ser definida da seguinte maneira:
Assim, temos que a fração molar de vapor na interface da bolha se torna a seguinte:
Substituindo os temos da equação pelos dados obtidos, temos:
Passo 5
Então a fração molar do vapor de água no centro da bolha em 2 s pode ser determinada a partir da seguinte equação:
O número Biot , neste caso, é infinito, pois uma concentração superficial especificada corresponde a um coeficiente de transferência de massa infinitamente grande . Então, as duas constantes na equação acima são determinadas na Tabela 4-1 como sendo e .
Além disso, , pois o ar está inicialmente seco. A fração molar do vapor de água no centro da bolha em é determinada substituindo os dados obtidos na equação acima. Assim temos:
Portanto, a fração molar do vapor de água no centro da bolha em é .
Ou seja, as bolhas de ar ficam saturadas quando saem do aquário.