Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 107
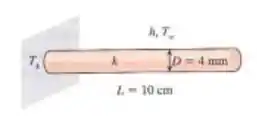
Obtenha a relação para eficiência da aleta para a transversal da área , constante, perímetro p, comprimento L e condutividade térmica k, exposta a convecção para o meio a com coeficiente de transferência de calor h. Considere que a aleta seja suficientemente longa para que a temperatura na sua ponta seja quase Tome a temperatura da aleta na base como sendo e despreze a transferência de calor a partir da sua ponta. Simplifica a relação para (a) aleta circular de diâmetro D e (b) aleta retangular de espessura t.
Passo 1
Beleza galera !!
Vamos começar a colocar em prática tudo que vimos na teoria!
Já sabemos que eficiência é dada por:
Considerando que a aleta seja suficientemente longa nós teremos que:
Agora, a taxa de transferência de calor ideal da aleta é dada por:
Lembrando que a área da aleta pode ser calculada como:
Vamos substituir tudo isso na fórmula do calor:
Simplificando:
E é isso aí !! Achamos o que precisávamos para dar continuidade no problema.
Passo 2
Agora vamos simplificar esta relação para uma aleta circular de diâmetro D, ok??
Para isso nós vamos precisar saber qual a relação da área da seção transversal e do perímetro com o diâmetro.
A área é fácil, vocês já sabem de cor, não é mesmo??
Mas e quanto ao perímetro??
Fácil!!
Agora é só colocarmos na fórmula que acabamos de achar:
Ainda dá pra simplificar mais:
Agora siiim, achamos a resposta para a letra (a)!!
Bora pra (b)??
Passo 3
Agora queremos a eficiência para uma aleta retangular de espessura t, não é?
E como faremos?
Mesma coisa !! Achamos a área da seção transversal e o perímetro em função da espessura.
Se chamarmos a largura dessa aleta de w, a área da seção transversal será dada simplesmente por:
E o perímetro para um retângulo?
Substituindo:
Considerando que a espessura é muito menor que a largura dessa aleta:
Finalizamos mais umaa !!