3- O papel da tensão superficial na formação de bolhas pode ser demonstrado considerando-se uma bolha esférica de vapor saturado puro em equilíbrio mecânico e térmico com seu líquido superaquecido.
- Iniciando com um esboço de uma bolha isolada, efetue um balanço de forças para obter uma expressão para o raio da bolha,
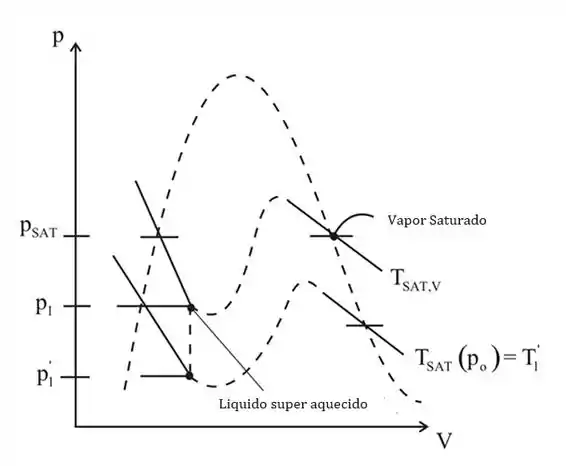
- Em um diagrama , represente os estados do líquido e da bolha. Discuta quais mudanças nessas condições causarão o aumento ou o colapso da bolha.
- Calcule o tamanho da bolha sob condições de equilíbrio nas quais o vapor está saturado a e a pressão no líquido corresponde a uma temperatura de saturação de .
sendo a pressão do vapor saturado e a pressão no líquido superaquecido externo à bolha.
Passo 1
Vamos calcular a força devido à tensão superficial usando a seguinte relação:
Aqui é o raio da bolha, é a pressão dentro da bolha e é a pressão fora da bolha.
Considere a seguinte relação para a força devido à tensão superficial:
Aqui é a tensão superficial.
Agora vamos igualas as equações (1) e (2).
Passo 2
Dentro da bolha, a pressão é a pressão de saturação; portanto, a pressão dentro da bolha será igual e, fora da bolha, existe líquido a pressão igual a ; portanto, a pressão fora da bolha será igual a .
Substituindo esses valores na equação , obtemos:
Portanto, o raio da bolha é .
Passo 3
b) Considere a figura a seguir, mostrando o diagrama:
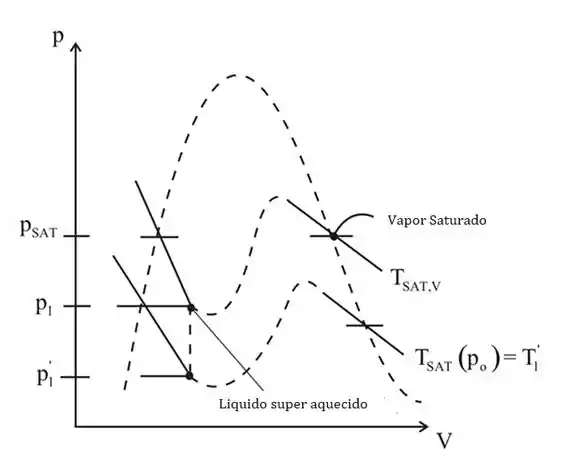
Passo 4
Aqui, para o equilíbrio térmico, a temperatura do líquido e do vapor deve ser a mesma, e para o equilíbrio mecânico, a pressão externa deve ser menor que a temperatura interna.
No diagrama , podemos observar que a bolha cresce à medida que o calor é transferido para ela.
A bolha entra em colapso quando e . Isso ocorre porque o vapor condensa à medida que o calor é transferido para fora da bolha.
Passo 5
c) Vamos considerar os seguintes dados:
Considere a pressão de saturação da água correspondente às temperaturas de saturação especificadas:
Considere a tensão superficial da água como .
Agora, vamos considerar a seguinte relação para o raio da bolha da peça .
Vamos substituir pelos valores conhecidos.
Portanto, o raio da bolha é .