21 – A partir do balanço de energia um elemento de volume de casca cilíndrica, derive a equação de condução de calor unidimensional permanente para um longo cilindro com condutividade térmica constante, no qual o calor é gerado a uma taxa
Passo 1
Considere que um elemento de casca cilíndrica fina de espessura r em um cilindro longo é como mostrado abaixo:
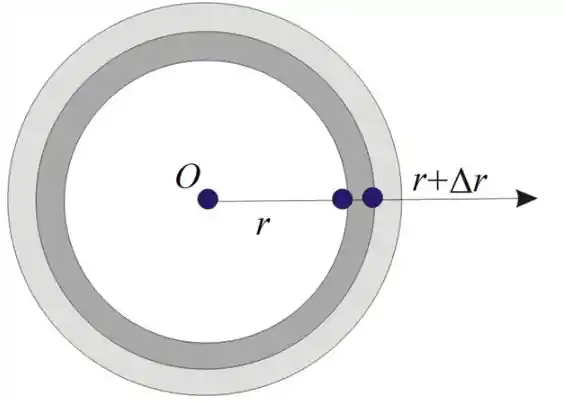
Passo 2
Considerações:
1) Unidimensional
2) estado estacionário
3) Condutividade térmica constante
4) Com geração interna de calor
Expresse a área do cilindro normal à direção da transferência de calor em qualquer local .
Aqui, é o comprimento do cilindro, é o raio do cilindro.
Como a área de transferência de calor depende de neste caso, então, o calor varia com o local.
Passo 3
Aplique o balanço energético a este elemento cilíndrico fino de espessura durante um pequeno intervalo de tempo .
Aqui, é a transferência de calor, é a geração interna de calor e é a energia interna.
Escreva a mudança na energia interna usando a expressão:
Aqui, é a densidade, é o calor específico do material, é o volume.
Passo 4
Vamos agora, substituir os valores conhecidos no balanço energético,
Dividindo os dois lados por temos:
Tomando os limites como e . Vamos dividir e resolver cada parte;
E a segunda parte,
Juntando as duas partes, temos que a equação (1) se torna
Substituindo
Aqui a propriedade é a difusividade térmica do material.
Portanto, a equação unidimensional de condução de calor com condutividade térmica constante e geração interna de calor no cilindro é
Resposta
Portanto, a equação unidimensional de condução de calor com condutividade térmica constante e geração interna de calor no cilindro é