Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 13

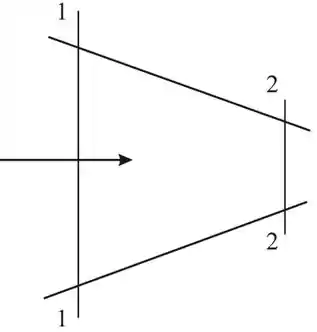
Ar, com pressão absoluta de 60,0   k P a e 27 ° C , entra em um canal a 486   m / s , onde A = 0,02   m 2 . Na seção 2 a jusante, p = 78,8   k P a   ( a b s ) . Considerando escoamento isentrópico, calcule o número de Mach na seção 2. Esboce a forma do canal.

Passo 1

Dado que o escoamento é isentrópico, temos as seguintes equações:

p 0 p 1 = 1 + k - 1 2 M 1 2 k k - 1  

p 0 p 2 = 1 + k - 1 2 M 2 2 k k - 1

Obtendo a razão das duas equações:

p 2 p 1 = 1 + k - 1 2 M 1 2 1 + k - 1 2 M 2 2 k k - 1

Calculando o número de Mach 1:

M 1 = V 1 c 1 = V 1 k R T 1

Sendo:

V 1 = 486   m / s ;

k a r = 1,4 ;

T 1 = 27 ° C = 300   K ;

R a r = 287 N ⋅ m k g ⋅ K .

Temos:

M 1 = 486 1,4 ⋅ 287 ⋅ 300 = 1,4

Passo 2

Calculando o número de Mach 2:

p 2 p 1 = 1 + k - 1 2 M 1 2 1 + k - 1 2 M 2 2 k k - 1

Sendo:

p 1 = 60,0   k P a ;

p 2 = 78,8   k P a   .

Temos:

78,8 60 = 1 + 1,4 - 1 2 ⋅ 1,4 2 1 + 1,4 - 1 2 M 2 2 1,4 1,4 - 1

1,313 = 1,392 1 + 0,2 M 2 2 3,5

1,081 + 0,2162 M 2 2 = 1,392

M 2 = 1,12

Passo 3

Esboce a forma do canal:

Resposta

M 2 = 1,12

Ver Outros Exercícios desse livro