Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 14.Problemas - Ex. 87
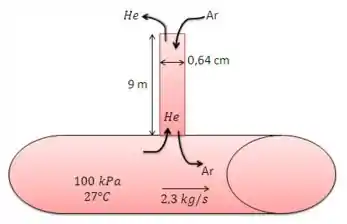
A pressão em um gasoduto que transporta gás hélio a uma taxa de 2,3 kg/s é mantida em 100 kPa, ventilando hélio para a atmosfera através de um tubo de 0,64 cm de diâmetro interno que se estende a 9 m no ar. Supondo que o hélio e o ar atmosférico estão a 27°C, determine (a) a taxa de fluxo de massa de hélio perdida para a atmosfera através do tubo, (b) a taxa de fluxo de massa do ar que se infiltra no gasoduto, e (c) a velocidade de escoamento na parte inferior do tubo, onde é anexado ao gasoduto que vai ser medido em operação constante por um anemômetro.
Passo 1
Vamos primeiro reunir nossos dados. Nosso composto A é hélio e o B é ar. As condições são e . Vamos considerar que o nosso processo de difusão vai do ponto em que o tubo é ligado à tubulação (z=0) até o final do tubo (z==9 m). O tubo tem diâmetro . Na posição z=0 há uma quantidade muito maior de hélio do que de ar, então . Ao final do tubo, há uma quantidade muito maior de ar do que hélio, então .
Além disso, o hélio e o ar se difundem em direções opostas e a uma mesma taxa, então trata-se de um processo de contradifusão equimolar (). Primeiro vamos calcular o fluxo molar e então convertê-lo em taxa de massa para o hélio e para o ar. Ao final, vamos usar as taxas mássicas para determinar a velocidade de escoamento da mistura na parte inferior do tubo. Vamos lá???
Passo 2
O fluxo molar para contradifusão equimolar é calculado por:
Precisamos então da difusividade e da concentração molar. A difusividade do hélio em ar é para e . Para obter a difusividade nas nossas condições podemos usar a relação:
A concentração molar para uma mistura gasosa é dada por:
O fluxo molar então é:
Para transformar o fluxo em taxa molar basta multiplicar pela área do tubo:
Como já comentamos
Passo 3
Nosso próximo passo é transformar as taxas molares e em taxas mássicas. Para isso precisamos das massas molares do hélio e do ar. Elas são:
A taxa mássica é dada por:
Para o hélio:
Para o ar:
Nosso último passo é determinar a velocidade na parte inferior do tubo. Para isso vamos usar:
Em que é a vazão mássica total na parte inferior do tubo. Sabemos que nessa região as vazões de hélio e ar são e . Então:
Além disso, na parte inferior do tubo a composição da mistura é praticamente 100 % hélio. Então . A velocidade é:
Resposta
A taxa de hélio perdido para a atmosfera é de ; a taxa de ar que entra no duto é de . A velocidade medida na parte inferior do tubo é .