Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 12.Problemas - Ex. 20

Em um processo isotérmico, 4,7 × 10–5 m3 de ar padrão por segundo é bombeado para um balão. A tensão na parede de borracha do balão é dada por σ = kA, na qual k = 31.416 N/m3 e A é a área da superfície do balão dada em m2. Calcule o tempo requerido para aumentar o raio do balão de 127 para 178 mm.

Passo 1

Vamos lá!!! A gente quer saber o tempo que vai levar para aumentar o raio do balão!!

Podemos fazer:

Δ t = Δ m m ˙

Sabendo que:

m ˙ = ρ Q

E:

ρ = p R T

Vamos fazer um esqueminha envolvendo as forças que agem sobre o balão:

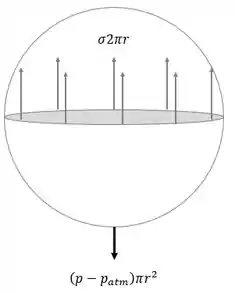
Para um sistema em equilíbrio:

p - p a t m π r 2 = σ 2 π r

O enunciado nos da:

σ = k A = k π r 2

Substituindo:

p - p a t m π r 2 = k ( 4 π r 2 ) 2 π r

Isolando a pressão:

p = p a t m + 8 π k r

Passo 2

Vamos calcular a vazão másica, considerando a pressão atmosférica e a temperatura de 20 ℃ , temos ρ = 1,21   k g / m 3 :

m ˙ = ρ Q

Substituindo e calculando:

m ˙ = 1,21 × 4,7 × 10 - 5 = 5,69 × 10 - 5 k g / s

Passo 3

Agora vamos calcular a massa para cada raio! Sabendo que:

p a t m = 101325   P a

V = 4 3 π r 2

Para r 1 = 128   m m = 0,128   m 3

p 1 = 101325 + 8 π 31416 0 , 128 = 202390   P a

ρ 1 = 202390   286,9 × 293 = 2 , 41   k g / m 3

V 1 = 4 3 π ( 0,1 2 8 ) 2 = 0,0 69   m 3

m 1 = 2 , 41 × 0,0 69 = 0 , 16 6   m 3

Para r 2 = 178   m m = 0,178   m , temos:

p 2 = 101325 + 8 π 31416 0,178 = 241868,5   P a

ρ 2 = 241868,5   286,9 × 293 = 2,88   k g / m 3

V 2 = 4 3 π ( 0,178 ) 2 = 0 , 133   m 3

m 2 = 2,88 × 0 , 133 = 0 , 38   m 3

Δ m = m 2 - m 1 = 0 , 38 - 0 , 166 = 0,214   k g

Δ t = Δ m m ˙

Δ t = 0,214 5,69 × 10 - 5 = 3761   s

Δ t = 62,6   m i n

Resposta

Δ t = 62,6   m i n

Ver Outros Exercícios desse livro